练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是（　　）
    A．A∈l，A∈α，B∈l，B∈α?l?α
    B．A∈α，A∈β，B∈α，B∈β?α∩β=直线AB
    C．l?α，A∈l?A?α
    D．C∈α，B、C∈β且A、B、C不共线?α与β重合
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    1、B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是（　　）
    A．A∈l，A∈α，B∈l，B∈α?l?α
    B．A∈α，A∈β，B∈α，B∈β?α∩β=直线AB
    C．l?α，A∈l?A∉α
    D．C∈α，B、C∈β且A、B、C不共线?α与β重合

    查看答案和解析>>

    科目：高中数学 来源：广东省高考数学一轮复习：10.6 空间图形的基本关系与公理（解析版） 题型：选择题

    B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是（ ）
    A．A∈l，A∈α，B∈l，B∈α⇒l?α
    B．A∈α，A∈β，B∈α，B∈β⇒α∩β=直线AB
    C．l?α，A∈l⇒A∉α
    D．C∈α，B、C∈β且A、B、C不共线⇒α与β重合

    查看答案和解析>>

    科目：高中数学 来源：高考数学一轮复习必备（第71课时）：第九章 直线、平面、简单几何体-平面的基本性质（解析版） 题型：选择题

    B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是（ ）
    A．A∈l，A∈α，B∈l，B∈α⇒l?α
    B．A∈α，A∈β，B∈α，B∈β⇒α∩β=直线AB
    C．l?α，A∈l⇒A∉α
    D．C∈α，B、C∈β且A、B、C不共线⇒α与β重合

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    B、C表示不同的点，a、l表示不同的直线，α、β表示不同的平面，下列推理不正确的是


    1. A.
      A∈l，A∈α，B∈l，B∈α?l?α
    2. B.
      A∈α，A∈β，B∈α，B∈β?α∩β=直线AB
    3. C.
      l?α，A∈l?A∉α
    4. D.
      C∈α，B、C∈β且A、B、C不共线?α与β重合

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省孝感高级中学高二（下）期中数学试卷（文科）（解析版） 题型：解答题

    已知点，动点N（x，y），设直线NP，NQ的斜率分别记为k1，k2，记（其中“?”可以是四则运算加、减、乘、除中的任意一种运算），坐标原点为O，点M（2，1）．
    （Ⅰ）探求动点N的轨迹方程；
    （Ⅱ）若“?”表示乘法，动点N的轨迹再加上P，Q两点记为曲线C，直线l平行于直线OM，且与曲线C交于A，B两个不同的点．
    （ⅰ）若原点O在以AB为直径的圆的内部，试求出直线l在y轴上的截距m的取值范围．
    （ⅱ）试求出△AOB面积的最大值及此时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：2007年上海市高三教学质量检测数学试卷(文) 题型：044

    在△ABC中，已知A(0，a)，B(0，－a)，(a为不等于零的常数)AC、BC两边所在的直线分别与x轴交于原点同侧的点M、N．设C(x0，y0)．

    (1)求M、N两点坐标(用(x0，y0)及α表示)．

    (2)若M、N满足，求点C的轨迹方程；

    (3)如果存在直线l∶y＝kx－1(k≠0)，使l与点C的轨迹相交于不同的P、Q两点，且，求α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

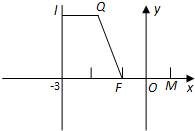    精英家教网已知点Q（x，y）位于直线x=-3右侧，且到点F（-1，0）与到直线x=-3的距离之和等于4．
    （1）求动点Q（x，y）的坐标之间满足的关系式，并化简且指出横坐标x的范围；
    （2）设（1）中的关系式表示的曲线为C，若直线l过点M（1，0）且交曲线C于不同的两点A、B，
        ①求直线l的斜率的取值范围；
        ②若点P满足
    FP
    =
    1
    2
    (
    FA
    +
    FB
    )    ，且
    EP
    .
    AB
    =0    ，其中点E的坐标为（x0，0）试求x0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    12、给定下列四个命题：
    （1）给定空间中的直线l及平面α，“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的充分不必要条件；
    （2）已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的必要不充分条件；
    （3）已知m，n是两条不同的直线，α，β是两个不同的平面，若m∥α，n∥β，m⊥n，则α⊥β；
    （4）在三棱柱ABC-A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是60°．
    上述命题中，真命题的序号是（　　）

    查看答案和解析>>

    科目：高中数学 来源：人教B版（新课标） 选修2-1 题型：

    已知点P(－2，0)，Q(2，0)，动点N(x，y)，直线NP，NQ的斜率分别为k1，k2，且(其中“”可以是四则运算加、减、乘、除中的任意一种运算)，坐标原点为O，点M(2，1)．

    (Ⅰ)探求动点N的轨迹方程；

    (Ⅱ)若“”表示乘法，动点N的轨迹再加上P，Q两点记为曲线C，直线l平行于直线OM，且与曲线C交于A，B两个不同的点．求ΔAOB的面积S的取值范围．

    查看答案和解析>>


    同步练习册答案