已知等差数列{a_n}的首项为4，公差为4，其前n项和为S_n，则数列 {}的前n项和为（　　）

已知等差数列{a_n}的首项为a₁，公差为d，其前n项和为S_n，若直线y＝a₁x与圆(x－2)²＋y²＝4的两个交点关于直线x＋y＋d＝0对称，则S_n＝________．

已知等差数列{an}的首项为a1，公差为d，其前n项和为Sn，若直线y＝a1x与圆(x－2)2＋y2＝4的两个交点关于直线x＋y＋d＝0对称，则Sn＝________．

已知等差数列{a_n}的首项为p，公差为d（d＞0）．对于不同的自然数n，直线x=a_n与x轴和指数函数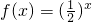的图象分别交于点A_n与B_n（如图所示），记B_n的坐标为（a_n，b_n），直角梯形A₁A₂B₂B₁、A₂A₃B₃B₂的面积分别为s₁和s₂，一般地记直角梯形A_nA_n+1B_n+1B_n的面积为s_n．
（1）求证数列{s_n}是公比绝对值小于1的等比数列；
（2）设{a_n}的公差d=1，是否存在这样的正整数n，构成以b_n，b_n+1，b_n+2为边长的三角形？并请说明理由；
（3）（理）设{a_n}的公差d（d＞0）为已知常数，是否存在这样的实数p使得（1）中无穷等比数列{s_n}各项的和S＞2010？并请说明理由．
（4）（文）设{a_n}的公差d=1，是否存在这样的实数p使得（1）中无穷等比数列{s_n}各项的和S＞2010？如果存在，给出一个符合条件的p值；如果不存在，请说明理由．