
平面上两个点A(0,1),B(0,6),动点P满足|PA|-|PB|=5,则点P的轨迹是( )
|
科目:高中数学 来源:不详 题型:单选题
| A.一条线段 | B.双曲线的一支 |
| C.一条射线 | D.椭圆 |
科目:高中数学 来源:2007-2008学年北京五中高三(上)12月数学试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:044
平面上两个质点
A、B分别位于(0,0),(2,2),在某一时刻同时开始,每隔1秒钟向上下左右任一方向移动1个单位,已知质点A向左右移动的概率都是![]() ,向上下移动的概率分别是
,向上下移动的概率分别是![]() 和
和![]() ,质点B向各个方向移动的概率是
,质点B向各个方向移动的概率是![]() ,
,
求:(1)4秒钟后A到达C(1,1)的概率;
(2)三秒钟后,A,B同时到达0(1,2)的概率.

科目:高中数学 来源:数学教研室 题型:044
A、B分别位于(0,0),(2,2),在某一时刻同时开始,每隔1秒钟向上下左右任一方向移动1个单位,已知质点A向左右移动的概率都是![]() ,向上下移动的概率分别是
,向上下移动的概率分别是![]() 和
和![]() ,质点B向各个方向移动的概率是
,质点B向各个方向移动的概率是![]() ,
,
求:(1)4秒钟后A到达C(1,1)的概率;
(2)三秒钟后,A,B同时到达0(1,2)的概率.
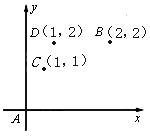
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 3 |
科目:高中数学 来源: 题型:解答题
科目:高中数学 来源:海淀区一模 题型:解答题
科目:高中数学 来源:浙江省模拟题 题型:解答题
 ,1)。
,1)。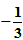 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由。
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com