
函数y=|x|的定义域为A,值域为B,若A={-1,0,1},则A∩B为( )
|
科目:高中数学 来源:2012年广西北海市高考数学一模试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源:2010年吉林省高二下学期期末考试理科数学卷 题型:选择题
函数f(x)的定义域为D,若满足:①f(x)在D上是单调函数;②存在 ,使得f(x)在[a,b]上的值域为[a,b],则y=f(x)叫做闭函数。现在
,使得f(x)在[a,b]上的值域为[a,b],则y=f(x)叫做闭函数。现在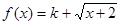 是闭函数,则k的取值范围是( )
是闭函数,则k的取值范围是( )
A. B.
B. 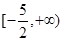 C.
C.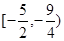 D.
D. 
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[-b,-a],那么y=f(x)叫做对称函数,现有f(x)= -k是对称函数,那么k的取值范围是________.
-k是对称函数,那么k的取值范围是________.
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
A.存在极大值 B.存在极小值
C.是增函数 D.是减函数
科目:高中数学 来源:专项题 题型:解答题
 ;
;科目:高中数学 来源: 题型:
①对任意x∈R,有f(x)>0;
②对任意x、y∈R,有f(xy)=[f(x)]y;
③f(![]() )>1.
)>1.
(1)求f(0)的值;
(2)求证:f(x)在R上是单调增函数;
(3)若a>b>c>0,且b2=ac,求证:f(a)+f(c)>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com