
一系列椭圆都以一定直线l为准线,所有椭圆的中心都在定点M,且点M到l的距离为2,若这一系列椭圆的离心率组成以
|
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 3 |
科目:高中数学 来源: 题型:
A.![]() [1-(
[1-(![]() )n-1] B.
)n-1] B. ![]() [1-(
[1-(![]() )n-1]
)n-1]
C. ![]() [1-(
[1-(![]() )n] D.
)n] D. ![]() [1-(
[1-(![]() )n]
)n]
科目:高中数学 来源: 题型:
A.![]() [1-(
[1-(![]() )n-1] B.
)n-1] B.![]() [1-(
[1-(![]() )n-1]
)n-1]
C.![]() [1-(
[1-(![]() )n] D.
)n] D.![]() [1-(
[1-(![]() )n]
)n]
科目:高中数学 来源:不详 题型:单选题
| 3 |
| 4 |
| 1 |
| 3 |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:2009年重庆十一中高考数学模拟试卷(10)(解析版) 题型:选择题
 为首项,
为首项, 为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=( )
为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=( )



科目:高中数学 来源: 题型:单选题
 为首项,
为首项, 为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=
为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=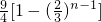
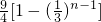
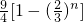
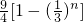
科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
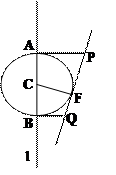
 如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
C过F的切线交于点P和点Q,则P、Q必在以F为焦点,l为准线的同一条抛物线上.
(Ⅰ)建立适当的坐标系,求出该抛物线的方程;
(Ⅱ)对以上结论的反向思考可以得到另一个命题:
“若过抛物线焦点F的直线与抛物线交于P、Q两点,
则以PQ为直径的圆一定与抛物线的准线l相切”请
问:此命题是否正确?试证明你的判断;
(Ⅲ)请选择椭圆或双曲线之一类比(Ⅱ)写出相应的命题并
证明其真假.(只选择一种曲线解答即可,若两种都选,则以第一选择为评分依据)
科目:高中数学 来源:不详 题型:解答题
科目:高中数学 来源:云南省红河哈尼族彝族自治州蒙自县高级中学2006-2007学年度高三数学理科第一次月考试卷 题型:013
一系列椭圆都以坐标原点为中心,以定直线l为准线,且中心到准线l的距离为2,若这一系列椭圆的离心率组成以![]() 为首项,
为首项,![]() 为公比的等比数列,而椭圆相应的长半轴长为ai,(i=1,2,3,…,n),则a1+a2+a3+…+an=
为公比的等比数列,而椭圆相应的长半轴长为ai,(i=1,2,3,…,n),则a1+a2+a3+…+an=
A.![]()
B.![]()
C.![]()
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com