
设函数f(x)=sin(ωx+φ),条件P:“f(0)=0”;条件Q:“f(x)为奇函数”,则P是Q的( )
|
科目:高中数学 来源:孝感模拟 题型:单选题
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
科目:高中数学 来源:2008-2009学年湖北省孝感市高三第二次统考数学试卷(文科)(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源: 题型:
| π |
| 8 |
| π |
| 8 |
科目:高中数学 来源:2011年江西省新余一中高考数学一模试卷(文科)(解析版) 题型:解答题
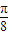 个单位即可得到函数
个单位即可得到函数 的图象;
的图象;科目:高中数学 来源: 题型:
| OP |
| OA |
| OB |
| OC |
| n |
 |
| i=1 |
科目:高中数学 来源:不详 题型:填空题
| OP |
| OA |
| OB |
| OC |
| n |
 |
| i=1 |
科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| n |
| π |
| 3 |
| π |
| 6 |
科目:高中数学 来源:2010年上海市普陀区高考数学二模试卷 (理科)(解析版) 题型:解答题
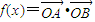 .
.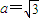 ,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;
,b=1,ω=2,求方程f(x)=1在区间[0,2π]内的解集;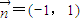 的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;
的直线l上的动点.当x∈R时,设函数f(x)的值域为集合M,不等式x2+mx<0的解集为集合P.若P⊆M恒成立,求实数m的最大值;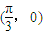 对称,且在
对称,且在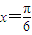 处f(x)取得最小值”.
处f(x)取得最小值”.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com