练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=
    x2+2x+2
    x+1
    (x＞-1)    的图象的最低点坐标是（　　）
    A．（0，2）B．不存在C．（1，2）D．（1，-2）
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    函数y=
    x2+2x+2
    x+1
    (x＞-1)    的图象的最低点坐标是（　　）
    A、（0，2）B、不存在
    C、（1，2）D、（1，-2）

    查看答案和解析>>

    科目：高中数学 来源：顺德区模拟 题型：单选题

    函数y=
    x2+2x+2
    x+1
    (x＞-1)    的图象的最低点坐标是（　　）
    A．（0，2）B．不存在C．（1，2）D．（1，-2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数y=f（x）的最小正周期为π，且图象关于点（
    π
    3
    ，0）对称，则f（x）的解析式可以是（　　）
    A、y=sin（
    x
    2
    +
    5π
    6
    ）
    B、y=sin（
    x
    2
    -
    5π
    6
    ）
    C、y=2sin2x-1
    D、y=cos（2x-＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞π6
    π
    6
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）求函数y=
    x2-2x+1
    x-2
      （x＜2）的最大值
    （2）函数y=loga（x+3）（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中mn＞0，求
    1
    m
    +
    2
    n
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市浦东新区高考数学三模试卷（理科）（解析版） 题型：解答题

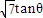    已知函数y=f（x），x∈D，y∈A；g（x）=x2-（4）x+1，
    （1）当f（x）=sin（x+φ）为偶函数时，求φ的值．
    （2）当f（x）=sin（2x+）+sin（2x+）时，g（x）在A上是单调递增函数，求θ的取值范围．
    （3）当f（x）=a1sin（ωx+φ1）+a2sin（ωx+φ2）+…+ansin（ωx+φn）时，（其中ai∈R，i=1，2，3…n，ω＞0），若f2（0）+f2（）≠0，且函数f（x）的图象关于点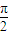（，0）对称，在x=π处取得最小值，试探讨ω应该满足的条件．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数y=f（x），x∈D，y∈A；g（x）=x2-（4
    		7
    tanθ    ）x+1，
    （1）当f（x）=sin（x+φ）为偶函数时，求φ的值．
    （2）当f（x）=sin（2x+
    π
    6
    ）+
    		3
    sin（2x+
    π
    3
    ）时，g（x）在A上是单调递增函数，求θ的取值范围．
    （3）当f（x）=a1sin（ωx+φ1）+a2sin（ωx+φ2）+…+ansin（ωx+φn）时，（其中ai∈R，i=1，2，3…n，ω＞0），若f2（0）+f2（
    π
    2ω
    ）≠0，且函数f（x）的图象关于点（
    π
    2
    ，0）对称，在x=π处取得最小值，试探讨ω应该满足的条件．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （1）求函数y=
    x2-2x+1
    x-2
    （x＜2）的最大值
    （2）函数y=loga（x+3）（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中mn＞0，求
    1
    m
    +
    2
    n
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源：山东省济宁市金乡二中2012届高三11月月考数学文科试题 题型：022

    有下列命题：①函数y＝f(－x＋2)与y＝f(x－2)的图象关于y轴对称；

    ②若函数f(x)＝ex，则，都有；

    ③若函数f(x)＝loga|x|(a＞0，a≠1)在(0，＋∞)上单调递增，则f(－2)＞f(a＋1)；

    ④若函数f(x＋2010)＝x2－2x－1(x∈R)，则函数f(x)的最小值为－2．

    其中真命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：江西省白鹭洲中学2012届高三第一次月考数学文科试题 题型：022

    有下列命题：

    ①函数y＝f(－x＋2)与y＝f(x－2)的图象关于y轴对称；

    ②若函数f(x)＝ex，则x1，x2∈R，都有；

    ③若函数f(x)＝loga|x|(a＞0，a≠1)在(0，＋∞)上单调递增，则f(－2)＞f(a＋1)；

    ④若函数f(x＋2010)＝x2－2x－1(x∈R)，则函数f(x)的最小值为－2．

    其中真命题的序号是________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•浦东新区三模）已知函数y=f（x），x∈D，y∈A；g（x）=x2-（4
    		7
    tanθ    ）x+1，
    （1）当f（x）=sin（x+φ）为偶函数时，求φ的值．
    （2）当f（x）=sin（2x+
    π
    6
    ）+
    		3
    sin（2x+
    π
    3
    ）时，g（x）在A上是单调递增函数，求θ的取值范围．
    （3）当f（x）=a1sin（ωx+φ1）+a2sin（ωx+φ2）+…+ansin（ωx+φn）时，（其中ai∈R，i=1，2，3…n，ω＞0），若f2（0）+f2（
    π
    2ω
    ）≠0，且函数f（x）的图象关于点（
    π
    2
    ，0）对称，在x=π处取得最小值，试探讨ω应该满足的条件．

    查看答案和解析>>


    同步练习册答案