
已知偶函数f(x)满足条件:当x∈R时,恒有f(x+2)=f(x),且0≤x≤1时,有f′(x)>0,则f(
|
科目:高中数学 来源: 题型:
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
科目:高中数学 来源:杭州一模 题型:单选题
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
A.f(
| B.f(
| ||||||||||||
C.f(
| D.f(
|
科目:高中数学 来源:2008年浙江省杭州市高考数学一模试卷(理科)(解析版) 题型:选择题
 ),f(
),f( ),f(
),f( )的大小关系是( )
)的大小关系是( ) )>f(
)>f(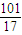 )>f(
)>f(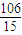 )
) )>f(
)>f( )>f(
)>f( )
) )>f(
)>f( )>f(
)>f( )
)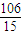 )>f(
)>f(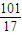 )>f(
)>f( )
)科目:高中数学 来源: 题型:单选题
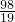 ),f(
),f(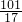 ),f(
),f(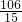 )的大小关系是
)的大小关系是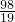 )>f(
)>f(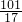 )>f(
)>f(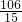 )
)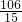 )>f(
)>f(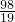 )>f(
)>f(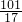 )
)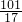 )>f(
)>f(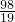 )>f(
)>f(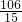 )
)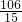 )>f(
)>f(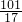 )>f(
)>f(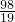 )
)科目:高中数学 来源: 题型:
| 1 |
| e2x |
| a |
| ex |
| x2 |
| a |
| 3 |
| a |
科目:高中数学 来源: 题型:
| f(x1)f(x2)+1 | f(x2)-f(x1) |
科目:高中数学 来源:2010年广东省广州市广雅中学高考数学模拟试卷(文科)(解析版) 题型:解答题
 ,其中a∈R.
,其中a∈R. ,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).科目:高中数学 来源:2009-2010学年辽宁省沈阳市东北育才学校高三(下)5月月考数学试卷(理科)(解析版) 题型:解答题
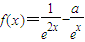 ,其中a∈R.
,其中a∈R. ,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).科目:高中数学 来源:不详 题型:解答题
| 1 |
| e2x |
| a |
| ex |
| x2 |
| a |
| 3 |
| a |
科目:高中数学 来源:2011-2012学年湖北省黄冈中学高一(上)期中数学试卷(解析版) 题型:解答题
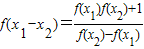 ;
;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com