
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )
 |
科目:高中物理 来源: 题型:
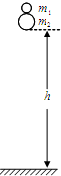 如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )科目:高中物理 来源:丰台区一模 题型:单选题
| A.h | B.2h | C.3h | D.4h |
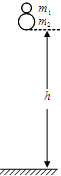
科目:高中物理 来源:2013年北京市丰台区高考物理一模试卷(解析版) 题型:选择题
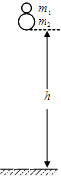
科目:高中物理 来源: 题型:
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向。已知m2=3m1,则小球m1反弹后能达到的高度为( )
A.h B.2h C.3h D.4h
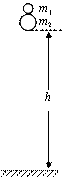
科目:高中物理 来源: 题型:
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向。已知m2=3m1,则小球m1反弹后能达到的高度为( )
A.h B.2h C.3h D.4h

科目:高中物理 来源:同步单元练习 高中1年级第二学期用 物理第一册 下 题型:038
如图所示,当质量分别为m1和m2的两球以等角速度ω绕轴在光滑平面上旋转时,烧断绳A的瞬间,m1的加速度大小是多少?方向怎样?(烧断绳A的瞬间m1离轴距离为l1,m1和m2间的距离为l2)

科目:高中物理 来源:2013-2014学年江西省赣州市六校高三上学期期末联考理综物理试卷(解析版) 题型:计算题
如图所示,两质量分别为M1=M2=1.0kg的木板和足够高的光滑凹槽静止放置在光滑水平面上,木板和光滑凹槽接触但不粘连,凹槽左端与木板等高。现有一质量m=2.0kg的物块以初速度vo=5.0m/s从木板左端滑上,物块离开木板时木板的速度大小为1.0m/s,物块以某一速度滑上凹槽。已知物块和木板间的动摩擦因数μ=0.5,重力加速度g取10m/s2。求:

Ⅰ.木板的长度;
Ⅱ.物块滑上凹槽的最大高度。
科目:高中物理 来源: 题型:计算题
如图所示,两质量分别为M1=M2=1.0kg的木板和足够高的光滑凹槽静止放置在光滑水平面上,木板和光滑凹槽接触但不粘连,凹槽左端与木板等高。现有一质量m=2.0kg的物块以初速度vo=5.0m/s从木板左端滑上,物块离开木板时木板的速度大小为1.0m/s,物块以某一速度滑上凹槽。已知物块和木板间的动摩擦因数μ=0.5,重力加速度g取10m/s2。求:
Ⅰ.木板的长度;
Ⅱ.物块滑上凹槽的最大高度。
科目:高中物理 来源: 题型:
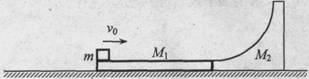
如图所示,两质量分别为M1=M2=1.0kg的木板和足够高的光滑凹槽静止放置在光滑水平面上,木板和光滑凹槽接触但不粘连,凹槽左端与木板等高.现有一质量m=2.0kg的物块以初速度V0=5.0m/s从木板左端滑上,物块离开木板时木板的速度大小为1.0m/s,物块以某一速度滑上凹槽.已知物块和木板间的动摩擦因数μ=0.5,重力加速度g取10m/s2.求:
①木板的长度;
②物块滑上凹槽的最大高度.
科目:高中物理 来源: 题型:
 两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.
两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com