
����Ŀ����4�֣���ͼ���������ܵ����ܳ�Ϊ360�ף��ס�������ͬʱ���������ܵ���A���������˳ʱ�뷽���н������ٶ�ʼ��Ϊ5��/�룻��������ٶ�Ϊ6��/�룬��һ�ι�����ٶȼ���![]() ���ڶ��ι�����ٶ�����
���ڶ��ι�����ٶ�����![]() �������ι�����ٶȼ���
�������ι�����ٶȼ���![]() �����Ĵι�����ٶ�����
�����Ĵι�����ٶ�����![]() �������ȥ�����ʣ������������ס������˵�1�������������ص��ںδ�����������������ǵ�100�������������ص��ںδ�����ע�⣺������һ��Ϊ��������
�������ȥ�����ʣ������������ס������˵�1�������������ص��ںδ�����������������ǵ�100�������������ص��ںδ�����ע�⣺������һ��Ϊ��������

���𰸡�������30���ס������˵�1�������������ص������D60�״���������360000�����ǵ�100�������������ص��ڵ�A����
��������
����������ҵ��ٶ�6����1��![]() ��=4��4��
��=4��4��![]() =6���ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6��A��Dʱ����D����18�룬������15�룬���ٶȱ�Ϊ4��/�룬����C��36�룬�ҵ���C��15+90��4=37.5�룬���Ե�һ������һ�����߶�DC��ijһ��������
=6���ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6��A��Dʱ����D����18�룬������15�룬���ٶȱ�Ϊ4��/�룬����C��36�룬�ҵ���C��15+90��4=37.5�룬���Ե�һ������һ�����߶�DC��ijһ��������
�ݴ������ڶ������߶�BC�ϵ��е�������
���������߶�AB�����A60�״�������
���Ĵ�ǡ���ڵ�D���������Ӵ˿�ʼ���������ң�����Ҫ��������ֻ���Ǽױ��Ҷ���һȦ���ݴ˽�ɣ�
�⣺��1���ҵ��ٶȣ�
6����1��![]() ��=4����/�룩��
��=4����/�룩��
4��![]() =6����/�룩��
=6����/�룩��
�����ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6
360��4=90���ף�
90��5=18���룩
90��6=15���룩
90��4=22.5���룩
�״ӵ�A����C�ã�18��2=36���룩��
�Ҵӵ�A����C�ã�15+22.5=37.5���룩
���Լ�������һ�����߶�DC��ijһ��������
��x���һ��������������ã�
90+5��x��18��=90+4��x��15��
��ã�x=30
30��5=150���ף�
150��90=60���ף�
�𣺳�����30���ס������˵�1�������������ص������D60�״���
��2����1��������DC�ϣ���2����CB�ϣ���3����BA�ϣ����Ĵ����������ڵ�D�ϣ���2Ȧ��2����D��������D�㿪ʼ����һֱ�����ң���˵�5��������Ȼֻ���Ǽױ��Ҷ�����һȦ��
�ҵ�ƽ���ٶ�=��90+90���£�90��6+90��4��=4.8����/�룩
��ʱ����£�360�£�5��4.8��=1800���룩
������1800��5��360=25��Ȧ��
������1800��75=24��Ȧ��
���Ե�5������֮��2�˻����֮ǰ�Ĺ��̣��ʵ�100������ʱ��Ϊ��
1800��20=360000���룩���ص���A��
�𣺳�����360000�����ǵ�100�������������ص��ڵ�A����


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ����Խ�������ڼ��г����ͳ��ͼ��
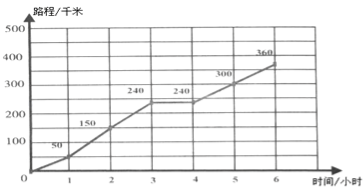
��1����Խ�����й����� ǧ����
��2������Ŀ�ĵ�ʱ������ Сʱ��;����Ϣ�� Сʱ��
��3��������Ϣ����Խ��ƽ��ÿСʱ�� ǧ����
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ����4�֣��С�Ů�����ᄊ�˶�Ա�ڳ�120��б������ϰ�ܲ�����ͼ���¶�ΪA���µ�Ϊ�У�����ͬʱ��A���������A��B֮�䲻ͣ���������ܣ���֪���˶�Ա�����ٶ���ÿ��3�ף������ٶ���ÿ��5�ף�Ů�˶�Ա�����ٶ���ÿ��2�ף������ٶ���ÿ��3�ף����ʣ����˵�һ��ӭ�������ĵص���A������ף��ڶ���ӭ�������ĵص���A������ף�

�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��һ��̣�������̨�����ڹ涨ʱ������ɣ��������2̨������ֻ���ù涨ʱ���![]() �Ϳ���ɣ��������2̨��������Ҫ�Ƴ�
�Ϳ���ɣ��������2̨��������Ҫ�Ƴ�![]() Сʱ������ɣ����ʣ�
Сʱ������ɣ����ʣ�
��1���ڹ涨ʱ��������輸̨������
��2����1̨����ȥ�����̣���Ҫ����Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��
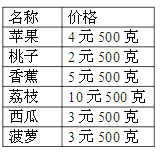
��1��ƻ���ļ۸������ӵļ�����
��2����֦�ļ۸����㽶�ļ�����
��3����2ǧ�˲�����Ҫ����Ǯ��
��4���������50Ԫȥ��ˮ������2500��ƻ����1ǧ����֦���������������ʣ����Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��������

�绰295Ԫ ���г�350Ԫ VCD690Ԫ �緹��365Ԫ �ֱ�280Ԫ
����������һ���ֱ���һ�����г�����Լ��Ҫ�� ��Ԫ��
��1000ԪǮ�������ļ���������
���㻹�������ʲô���⣿
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ�����
5����=���� ����������40����=����![]() ������
������
7����=���� ������ 30����=���� ������
8����=���� ����������100����=���� ������
37������17����=�� ��������=���� ������
45����+55����=���� ������=���� ������
�鿴�𰸺ͽ���>>
��Ŀ��Сѧ��ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ��ˮ�ɻ������װ��ˮ�IJ���ƿ�ڣ�ÿ��һ��۲�һ�Σ�����ѿ���ij��ȣ���������Ƴ��������ͳ��ͼ��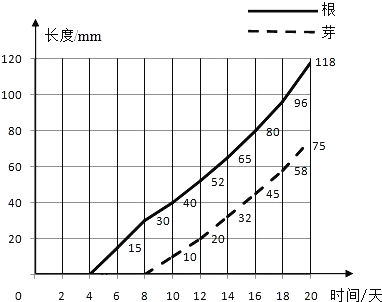
��1��С���ǵڼ��쿪ʼ����ѿ���ڼ��쿪ʼ�������ģ�
��2��˵˵ˮ�ɻ�ѿ���������仯�����
��3��������һ��ֲ�����ӣ���һ��������ʵ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com