
【题目】如图,点E在等边△ABC的边BC上,BE=6,射线CD⊥BC于点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+PF的值最小时,BF=7,则AC为______.

 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
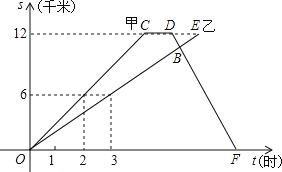
【题目】甲、乙两名同学进行登山比赛,甲同学和乙同学沿相同的路线同时在早8:00从山脚出发前往山顶,甲同学到达山顶后休息1小时,沿原路以每小时6千米的速度下山,在这一过程中,各自行进的路程随所用时间变化的图象如图所示,根据提供信息得出以下四个结论:
![]() 甲同学从山脚到达山顶的路程为12千米;
甲同学从山脚到达山顶的路程为12千米;
![]() 乙同学登山共用4小时;
乙同学登山共用4小时;
![]() 甲同学在14:00返回山脚;
甲同学在14:00返回山脚;
![]() 甲同学返回与乙同学相遇时,乙同学距登到山顶还有
甲同学返回与乙同学相遇时,乙同学距登到山顶还有![]() 千米的路程.
千米的路程.
以上四个结论正确的有![]()
![]() 个
个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系 ;
(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;
(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为![]() ,到y轴的距离为
,到y轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点P的最大距离;若
为点P的最大距离;若![]() ,则称
,则称![]() 为点P的最大距离.
为点P的最大距离.
例如:点P(![]() ,
,![]() )到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为![]() .
.
(1)①点A(2,![]() )的最大距离为 ;
)的最大距离为 ;
②若点B(![]() ,
,![]() )的最大距离为
)的最大距离为![]() ,则
,则![]() 的值为 ;
的值为 ;
(2)若点C在直线![]() 上,且点C的最大距离为
上,且点C的最大距离为![]() ,求点C的坐标;
,求点C的坐标;

(3)若⊙O上存在点M,使点M的最大距离为![]() ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因商人、商业、商品发源于商丘,商朝建都于河南商丘,商丘被誉为“三商之源,华商之都”![]() 商字是商丘市的城市地标,坐落在河南省商丘市睢阳区神火大道与南京路交汇处中的环岛内,雕塑建成与1997年6月29日,某中学九年级数学兴趣小组想测量商字雕塑AB的高度,小明在雕塑前一座写字楼CD分E处仰望商字雕塑的顶端A,测得仰角为
商字是商丘市的城市地标,坐落在河南省商丘市睢阳区神火大道与南京路交汇处中的环岛内,雕塑建成与1997年6月29日,某中学九年级数学兴趣小组想测量商字雕塑AB的高度,小明在雕塑前一座写字楼CD分E处仰望商字雕塑的顶端A,测得仰角为![]() ,小亮在写字楼前F处,测得商字雕塑的顶端A的仰角为
,小亮在写字楼前F处,测得商字雕塑的顶端A的仰角为![]() ,有装B,F,D在同一条直线上,
,有装B,F,D在同一条直线上,![]() ,
,![]() ,求商字雕塑AB的高度
,求商字雕塑AB的高度![]() 测角器的高度忽略不计,结果精确到1米
测角器的高度忽略不计,结果精确到1米![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①垂线段最短;
②一对内错角的角平分线互相平行;
③平面内的n条直线最多有![]() 个交点;
个交点;
④若![]() ,则
,则![]() ;
;
⑤平行于同一直线的两条直线互相平行,垂直于同一直线的两条直线也互相平行.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD和正方形EFGH的中心重合,![]() ,
,![]() ,
,![]() 分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,
分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,![]() 若
若![]() ,则AI的长为______,四边形AIEL的面积为______.
,则AI的长为______,四边形AIEL的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com