
 如图,△ABC中边BC=50,高AD=40,点E、F在AB、AC上,且EF∥BC交中线AM和高AD于点N和点G.
如图,△ABC中边BC=50,高AD=40,点E、F在AB、AC上,且EF∥BC交中线AM和高AD于点N和点G.分析 (1)由三角形重心的性质可知:$\frac{AN}{AM}=\frac{2}{3}$,从而可得到EF=$\frac{2}{3}CB$,DG=$\frac{1}{3}AD$,然后利用三角形的面积公式求解即可;
(2)设EF=x,由$\frac{EF}{CB}=\frac{AG}{AG}$,可求得AG=$\frac{4}{5}x$,然后可表示出GD=40-$\frac{4}{5}x$,由三角形的面积公式可求得△EDF的面积与x的函数关系,根据二次函数的性质可求得EF的长度.
解答 解:(1)∵N是三角形的重心,
∴$\frac{AN}{AM}=\frac{2}{3}$.
∵EF∥BC,
∴$\frac{EF}{CB}=\frac{2}{3}$,$\frac{DG}{AD}=\frac{1}{3}$.
∴EF=$\frac{2}{3}×50$=$\frac{100}{3}$,$DG=\frac{1}{3}×40$=$\frac{40}{3}$.
∴△EDF的面积=$\frac{1}{2}×\frac{100}{3}×\frac{40}{3}$=$\frac{2000}{9}$.
(2)设EF=x.
∵EF∥BC,
∴$\frac{EF}{CB}=\frac{AG}{AD}$,即$\frac{x}{50}=\frac{AG}{40}$.
∴AG=$\frac{4}{5}x$.
∴GD=40-AG=40-$\frac{4}{5}x$.
∴${S}_{△EFD}=\frac{1}{2}×EF×DG$=$\frac{1}{2}x(40-\frac{4}{5}x)$=$-\frac{2}{5}{x}^{2}+20x$.
∴x=-$\frac{b}{2a}$=$-\frac{20}{-2×\frac{2}{5}}$=25.
∴当EF=25时,△EDF的面积最大.
点评 本题主要考查的是相似三角形的性质和判定、二次函数的性质、三角形的重心,根据题意得出△EFD的面积与EF的长度的关系是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
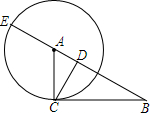 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{8}$ | B. | $\sqrt{8}$ | C. | $\frac{22}{7}$ | D. | 3.1415926 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com