
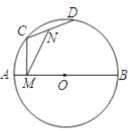
【题目】如图,![]() 为直径,
为直径,![]() ,
,![]() 、
、![]() 为圆上两个动点,
为圆上两个动点,![]() 为
为![]() 中点,
中点,![]() 于
于![]() ,当
,当![]() 、
、![]() 在圆上运动时保持
在圆上运动时保持![]() ,则
,则![]() 的长( )
的长( )
A.随![]() 、
、![]() 的运动位置而变化,且最大值为4
的运动位置而变化,且最大值为4
B.随![]() 、
、![]() 的运动位置而变化,且最小值为2
的运动位置而变化,且最小值为2
C.随![]() 、
、![]() 的运动位置长度保持不变,等于2
的运动位置长度保持不变,等于2
D.随![]() 、
、![]() 的运动位置而变化,没有最值
的运动位置而变化,没有最值
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
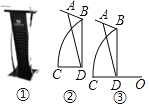
【题目】图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.7);
≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在去年的体育中考中,某校6名学生的体育成绩统计如下表:
成绩 | 17 | 18 | 20 |
人数 | 2 | 3 | 1 |
则下列关于这组数据的说法错误的是( )
A.众数是18B.中位数是18C.平均数是18D.方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵![]() 元,用
元,用![]() 元购进乙书包的个数与用
元购进乙书包的个数与用![]() 元购进甲书包的个数相等.
元购进甲书包的个数相等.
(1)求甲、乙两种书包的进价分别为多少元?
(2)商户购进甲、乙两种书包共![]() 个进行试销,其中甲书包的个数不少于
个进行试销,其中甲书包的个数不少于![]() 个,且甲书包的个数 的
个,且甲书包的个数 的![]() 倍不大于乙书包的个数,已知甲书包的售价为
倍不大于乙书包的个数,已知甲书包的售价为![]() 元/个,乙书包的售价为
元/个,乙书包的售价为![]() 元/个,且 全部售出,设购进甲书包
元/个,且 全部售出,设购进甲书包![]() 个,求该商店销售这批书包的利润
个,求该商店销售这批书包的利润![]() 与
与![]() 之间的函数关系式,并 写出
之间的函数关系式,并 写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,该店将![]() 个书包全部售出后,使用所获的利润又购进
个书包全部售出后,使用所获的利润又购进![]() 个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利
个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利![]() 元.请求出该店第二次进货所选用的进货方案?
元.请求出该店第二次进货所选用的进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
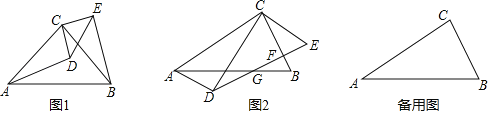
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() .
.
(1)若点![]() 也在该抛物线上,请用含
也在该抛物线上,请用含![]() 的关系式表示
的关系式表示![]() ;
;
(2)若该抛物线上任意不同两点![]() 、
、![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;若以原点
;若以原点![]() 为圆心,
为圆心,![]() 为半径的圆与抛物线的另两个交点为
为半径的圆与抛物线的另两个交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),且
左侧),且![]() 有一个内角为
有一个内角为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)在(2)的条件下,若点![]() 与点
与点![]() 关于点
关于点![]() 对称,且
对称,且![]() 、
、![]() 、
、![]() 三点共线,求证:
三点共线,求证:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
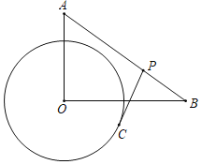
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PC(点C为切点),则线段PC长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com