
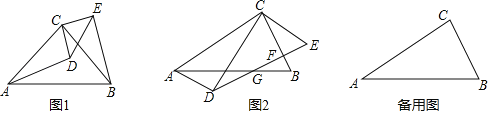
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
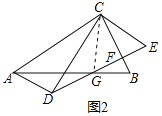
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
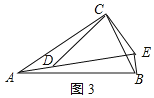
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
【答案】(1)见解析;(2)①![]() ;②BE的长为﹣2
;②BE的长为﹣2![]() +
+![]() 或
或![]() .
.
【解析】
(1)由等腰直角三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE,证出∠ACD=∠BCE,由SAS得出△ACD≌△BCE即可;
(2)①连接CG,由平行四边形的性质得出∠ADE+∠CED=180°,证出∠ADC=∠ADE﹣∠CDE=90°,A、D、G、C四点共圆,由圆周角定理得出∠AGC=∠ADC=90°,由直角三角形的性质得出CG=![]() AC,AG=
AC,AG=![]() CG,CG=
CG,CG=![]() BG,即可得出结果;
BG,即可得出结果;
②分三种情况:
当∠BED=90°时,证明△ACD∽△BCE,得出![]() =
=![]() ,得出AD=
,得出AD=![]() BE,证出A、D、E共线,在Rt△ABE中,由勾股定理得出方程,解方程即可;
BE,证出A、D、E共线,在Rt△ABE中,由勾股定理得出方程,解方程即可;
当∠DBE=90°时,作CF⊥AB于F,由勾股定理得出DF=![]() ,得出AD=
,得出AD=![]() ,即可得出BE的长;
,即可得出BE的长;
当∠BDE=90°时,作BG⊥CD于G,设DG=x,则CG=4![]() ﹣x,BG=
﹣x,BG=![]() x,在Rt△BCG中,由勾股定理得出方程,解方程即可.
x,在Rt△BCG中,由勾股定理得出方程,解方程即可.
(1)证明:∵△ABC和△CDE是两个等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,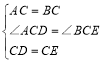 ,
,
∴△ACD≌△BCE(SAS);
(2)解:①连接CG,如图2所示:
∵四边形ADEC为平行四边形,
∴AD∥CE,
∴∠ADE+∠CED=180°,
∵∠CED=90°﹣∠CDE=90°﹣30°=60°,
∴∠ADE=120°,
∴∠ADC=∠ADE﹣∠CDE=90°,
∵∠CAB=∠CDE=30°,
∴A、D、G、C四点共圆,
∴∠AGC=∠ADC=90°,
∵∠CAB=30°,
∴CG=![]() AC,AG=
AC,AG=![]() CG,∠BCG=30°,
CG,∠BCG=30°,
∴CG=![]() BG,即BG=
BG,即BG=![]() CG,
CG,
∴![]() =3;
=3;
②分三种情况:
当∠BED=90°时,如图3所示:
∵△ABC和△CDE是两个含30°的直角三角形,∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,
∴∠ACD=∠BCE,![]() ,
,
∴△ACD∽△BCE,
∴![]() =
=![]() ,
,
∴AD=![]() BE,
BE,
∴∠ADC=∠BEC=90°+∠CED=90°+60°=150°,
∵∠CDE=30°,
∴∠CDE+∠ADC=180°,
∴A、D、E共线,
在Rt△ABE中,由勾股定理得:AE2+BE2=AB2,
即(![]() BE+8)2+BE2=102,
BE+8)2+BE2=102,
解得:BE=﹣2![]() ±
±![]() (负值舍去),
(负值舍去),
∴BE=﹣2![]() +
+![]() ;
;
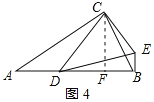
当∠DBE=90°时,如图4所示:
作CF⊥AB于F,则∠BCF=30°,
∴BF=![]() BC,
BC,
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,
∴BC=![]() AB=5,CE
AB=5,CE![]() DE=4,
DE=4,
∴CD=![]() CE=4
CE=4![]() ,
,
∴BF=![]() BC=
BC=![]() ,
,
∴CF=![]() BF=
BF=![]()
![]() ,
,
∴DF=![]() ,
,
∵AB=AD+DF+BF,
∴AD=10﹣![]() ,
,
∴BE=![]() ;
;
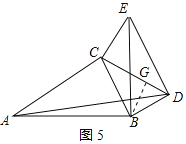
当∠BDE=90°时,如图5所示:
作BG⊥CD于G,
则∠BDG=∠BDE﹣∠CDE=60°,
∴∠DBG=30°,
∴BD=2DG,BG=![]() DG,
DG,
设DG=x,则CG=4![]() ﹣x,BG=
﹣x,BG=![]() x,
x,
在Rt△BCG中,由勾股定理得:CG2+BG2=BC2,
即(4![]() ﹣x)2+(
﹣x)2+(![]() x)2=52,
x)2=52,
整理得:4x![]() x+23=0,
x+23=0,
∵△=(﹣8![]() )2﹣4×4×23<0,
)2﹣4×4×23<0,
∴此方程无解;
综上所述,当以点B、D、E为顶点的三角形是直角三角形时,BE的长为﹣2![]() +
+![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
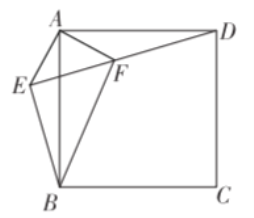
【题目】如图,![]() 是正方形
是正方形![]() 外一点,连接
外一点,连接![]() 交
交 ![]() 于点
于点![]() ,若
,若![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③ 四边形
;③ 四边形![]() 的面积是
的面积是![]() ;④点
;④点![]() 到 直线
到 直线![]() 的距离为
的距离为![]() ;⑤
;⑤![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.![]() B.2C.3D.4
B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
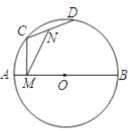
【题目】如图,![]() 为直径,
为直径,![]() ,
,![]() 、
、![]() 为圆上两个动点,
为圆上两个动点,![]() 为
为![]() 中点,
中点,![]() 于
于![]() ,当
,当![]() 、
、![]() 在圆上运动时保持
在圆上运动时保持![]() ,则
,则![]() 的长( )
的长( )
A.随![]() 、
、![]() 的运动位置而变化,且最大值为4
的运动位置而变化,且最大值为4
B.随![]() 、
、![]() 的运动位置而变化,且最小值为2
的运动位置而变化,且最小值为2
C.随![]() 、
、![]() 的运动位置长度保持不变,等于2
的运动位置长度保持不变,等于2
D.随![]() 、
、![]() 的运动位置而变化,没有最值
的运动位置而变化,没有最值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有六个完全相同的小球,小球上分别标有1,2,5,7,8,13六个数,搅匀后一次从中摸出一个小球,将小球上的数记为m,则使得一次函数y=(﹣m+1)x+11﹣m经过一、二、四象限且关于x的分式方程![]() =3x+
=3x+![]() 的解为整数的概率是( )
的解为整数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)将△ABC绕着O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1,并写出A1的坐标;
(2)以原点O为位似中心,在第一象限画出△A1B1C1的位似图形△A2B2C2,相似比为1:2,并写出A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
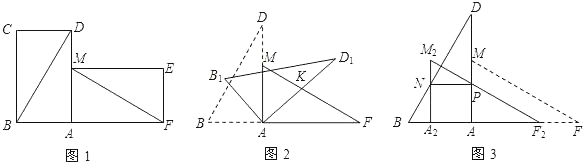
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30°.
(1)试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,求β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com