
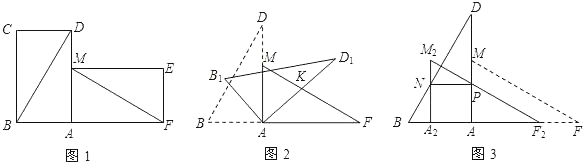
����Ŀ����������ȫ�غϵľ���ֽƬ��������һ���Ƶ�A˳ʱ����ת90����õ�����AMEF����ͼ1��������BD��MF����BD��16cm����ADB��30����
��1����̽���߶�BD ���߶�MF��������ϵ��λ�ù�ϵ����˵�����ɣ�
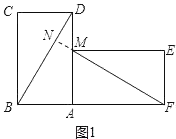
��2������BCD ����MEF ��ȥ������ABD�Ƶ�A˳ʱ����ת����AB1D1����AD1��FM �ڵ�K����ͼ2��������ת��Ϊ����0��������90����������AFK Ϊ����������ʱ�������Ķ�����
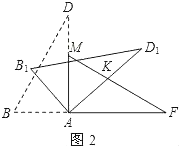
��3��������AFM��AB����ƽ�Ƶõ���A2F2M2����ͼ3����F2M2��AD���ڵ�P��A2M2��BD���ڵ�N����NP��ABʱ����ƽ�Ƶľ��룮
���𰸡���1��BD��MF��BD��MF�����ɼ���������2�����Ķ���Ϊ60����15������3��ƽ�Ƶľ����ǣ�12��4![]() ��cm��
��cm��
��������
��1���ӳ�FM��BD�ڵ�N������ת�����ʵ���BAD�ա�MAF���Ƴ�BD��MF����ADB����AFM�������ɵá�DNM��90����
��2���������������ۣ��ٵ�AK��FKʱ���ڵ�AF��FKʱ��������ת��������⼴�ɣ�
��3��ƽ�Ƶľ�����A2A�ij��ȣ��ھ���PNA2A�У�A2A��PN�����PN�ij��ȼ��ɣ�����DPN�ס�DAB�ó���Ӧ�߶γɱ��������ɵõ�A2A�Ĵ�С��
�⣺��1�����ۣ�BD��MF��BD��MF��
���ɣ���ͼ1���ӳ�FM��BD�ڵ�N��
������ã���BAD�ա�MAF��
��BD��MF����ADB����AFM��
�֡ߡ�DMN����AMF��
���ADB+��DMN����AFM+��AMF��90����
���DNM��90����
��BD��MF��
��2����ͼ2��
�ٵ�AK��FKʱ����KAF����F��30����
���BAB1��180������B1AD1����KAF��180����90����30����60����
������60����
�ڵ�AF��FKʱ����FAK��![]() ��180������F����75����
��180������F����75����
���BAB1��90������FAK��15����
������15����
�������������Ķ���Ϊ60����15����
��3����ͼ3��
������þ���PNA2A����A2A��x����PN��x��
��Rt��A2M2F2����F2M2��FM��16����A2F2M2����ADB��30����
��A2M2��8��A2F2��8![]() ��
��
��AF2��8![]() ��x��
��x��
�ߡ�PAF2��90������PF2A��30����
��AP��AF2tan30����8��![]() x��
x��
��PD��AD��AP��8![]() ��8+
��8+![]() x��
x��
���DPN�ס�DAB��
��![]() ��
��
��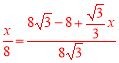 ��
��
���x��12��4![]() ����A2A��12��4
����A2A��12��4![]() ��
��
��ƽ�Ƶľ����ǣ�12��4![]() ��cm��
��cm��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
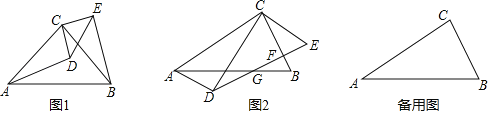
����Ŀ����1����ABC�͡�CDE����������ֱ�������Σ���ͼ1�����С�ACB����DCE��90�㣬����AD��BE����֤����ACD�ա�BCE��
��2����ABC�͡�CDE��������30���ֱ�������Σ����С�ACB����DCE��90�㣬��CAB����CDE��30�㣬CD��AC����CDE�ӱ�CD��AC�غϿ�ʼ�Ƶ�C��ʱ����תһ���Ƕ�����0�㣼����180�㣩��
����ͼ2��DE��BC���ڵ�F����AB���ڵ�G������AD�����ı���ADECΪƽ���ı��Σ���![]() ��ֵ��
��ֵ��
����AB��10��DE��8������BD��BE�����Ե�B��D��EΪ�������������ֱ��������ʱ����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У���
����![]() ������
������![]() ��
��![]() ��
��
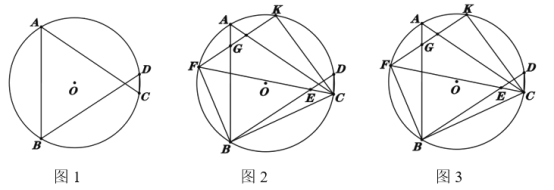
��1����ͼ1����֤��![]() ��
��
��2����ͼ2�����߶�![]() ��ȡ��
��ȡ��![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ������ֵ��
������ֵ��
��3����ͼ3���ڣ�2���������£�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ס��ҡ�����λͬѧ���5����ѧ�ɼ��������ڰ༶��Ӧƽ���ֵ�����ͳ��ͼ���������жϴ������( ).

A. ����ѧ�ɼ����ڰ༶ƽ���֣��ҳɼ��Ƚ��ȶ�
B. �ҵ���ѧ�ɼ��ڰ༶ƽ���ָ����������ұȱ���
C. ������ѧ�ɼ����ڰ༶ƽ���֣����ɼ�������
D. �ͼס��ҡ��������˶��ԣ��ҵ���ѧ�ɼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Կ����ڼ䣬�Ŷ��շѷ������£�������30��ʱ���˾��շ�120Ԫ������30���Ҳ�����m��30��m��100����ʱ��ÿ����1�ˣ��˾��շѽ���1Ԫ������m��ʱ���˾��շѶ�����m��ʱ�ı����辰��Ӵ���x���ο͵�ij�Ŷӣ���ȡ�ܷ���ΪyԪ��
��1����y����x�ĺ�������ʽ��
��2�����㹤����Ա���֣����Ӵ�ij�Ŷ���������һ������ʱ�����������������������ȡ���ܷ��÷���������һ����Ϊ������ȡ���ܷ��������Ŷ������������Ӷ����ӣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AD�ǡ�ABC������P���߶�AD�ϵ�һ�㣨�����A��D�غϣ�������PB��PC��E��F��G��H�ֱ���AB��AC��PB��PC���е㣬AD��EF���ڵ�M��
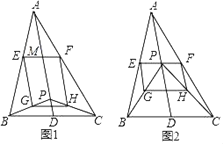
��1����ͼ1����AB��ACʱ����֤���ı���EGHF�Ǿ��Σ�
��2����ͼ2������P���M�غ�ʱ���ڲ������κθ����ߵ������£�д���������BPE�����ȵ������Σ���������BPE��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����ACΪֱ������O��BC�ڵ�D����AB�ڵ�E������D��DF��AB������ΪF������DE��
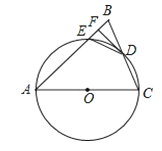
��1����֤��ֱ��DF����O���У�
��2����AE=7��BC=6����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA�С�O�ڵ�A��PC����O�����O����B��C���㣬��PA=6cm��PB=2![]() cm�����PAC�������_____cm2��
cm�����PAC�������_____cm2��
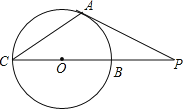
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com