
【题目】已知,在![]() 中,弦
中,弦![]() ,连接
,连接![]() 、
、![]() ;
;
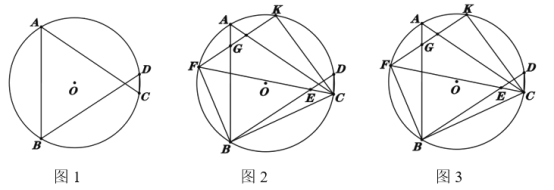
(1)如图1,求证:![]() ;
;
(2)如图2,在线段![]() 上取点
上取点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() ,求
,求![]() 的正切值;
的正切值;
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)tan∠BCF=![]() ;(3)
;(3)![]()
【解析】
(1)根据平行线的性质可得∠B=∠D,然后根据圆的基本性质可得![]() ,然后根据等式的基本性质即可证出
,然后根据等式的基本性质即可证出![]() ,最后根据圆的基本性质即可求出结论;
,最后根据圆的基本性质即可求出结论;
(2)过点K作KH⊥CD交CD的延长线于H,连接KD,根据等弧所对的圆周角相等可证∠BCF=∠DCK,从而得出tan∠BCF=tan∠DCK,设CK=5a,则DK=![]() a,然后根据圆内接四边形的性质、等腰直角三角形的性质、锐角三角函数和勾股定理即可求出tan∠DCK,从而求出结论;
a,然后根据圆内接四边形的性质、等腰直角三角形的性质、锐角三角函数和勾股定理即可求出tan∠DCK,从而求出结论;
(3)在(2)的图上延长FK和CH,交于点M,用含a的式子求出CK、BF和KH,然后证出△CKM∽△CBF,最后列出比例式即可求出结论.
解:(1)∵![]()
∴∠B=∠D
∴![]()
∴![]()
∴![]()
∴![]() ;
;
(2)过点K作KH⊥CD交CD的延长线于H,连接KD,
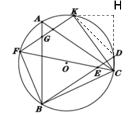
∵![]()
∴![]() ,∠KFC=∠BEF=45°
,∠KFC=∠BEF=45°
∴BF=DK,∠BCF=∠DCK
∴tan∠BCF=tan∠DCK
∵![]() ,∠HDK为圆内接四边形CDKF的外角
,∠HDK为圆内接四边形CDKF的外角
∴![]() ,∠HDK=∠KFC=45°
,∠HDK=∠KFC=45°
∴△DKH为等腰直角三角形
设CK=5a,则DK=![]() a,
a,
∴DH=HK=DK·sin∠HDK=3a
在Rt△CKH中,CH=![]() a
a
∴tan∠DCK=![]()
∴tan∠BCF=![]()
(3)在(2)的图上延长FK和CH,交于点M
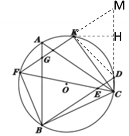
由(2)知:CK=5a,DH=HK=3a, BF=DK=![]() a,∠BCF=∠DCK
a,∠BCF=∠DCK
∵CD∥AB,FK∥BD
∴四边形GBDM为平行四边形
∴BG=DM
∵![]() =5a
=5a
∴DM=5a
∴MH=DM-DH=2a
在Rt△MKH中,KM=![]()
∵∠CKM为圆内接四边形FBCK的外角
∴∠CKM=∠CBF
∴△CKM∽△CBF
∴![]()
即![]()
解得:a=![]()
∴CK=5×![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有六个完全相同的小球,小球上分别标有1,2,5,7,8,13六个数,搅匀后一次从中摸出一个小球,将小球上的数记为m,则使得一次函数y=(﹣m+1)x+11﹣m经过一、二、四象限且关于x的分式方程![]() =3x+
=3x+![]() 的解为整数的概率是( )
的解为整数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)将△ABC绕着O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1,并写出A1的坐标;
(2)以原点O为位似中心,在第一象限画出△A1B1C1的位似图形△A2B2C2,相似比为1:2,并写出A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.

(1)当∠BAC=30时,求△ABC的面积;
(2)当DE=8时,求线段EF的长;
(3)在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
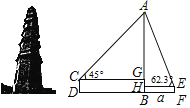
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
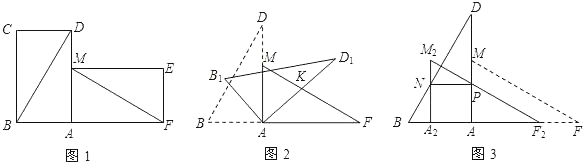
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30°.
(1)试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,求β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,根据习俗每家每户都会在门口挂灯笼和对联,某商店看准了商机,购进了一批红灯笼和对联进行销售,已知每幅对联的进价比每个红灯笼的进价少10元,且用480元购进对联的幅数是用同样金额购进红灯笼个数的6倍.
(1)求每幅对联和每个红灯笼的进价分别是多少?
(2)由于销售火爆,第一批销售完了以后,该商店用相同的价格再购进300幅对联和200个红灯笼,已知对联售价为6元一幅,红灯笼售价为24元一个,销售一段时间后,对联卖出了总数的![]() ,红灯笼售出了总数的
,红灯笼售出了总数的![]() ,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com