
【题目】如图,四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求证,四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() .求
.求![]() 的面积.
的面积.

【答案】(1)证明见详解;(2)12
【解析】
(1)根据平行四边形的判定定理得到四边形ABCD是平行四边形,根据三角形的外角的性质得到∠AOB=∠DAO+∠ADO=2∠OAD,求得∠DAO=∠ADO,推出AC=BD,于是得到四边形ABCD是矩形;
(2)根据![]() ,设AB=3x,则AD=4x,求出x的值,再求
,设AB=3x,则AD=4x,求出x的值,再求![]() 的面积即可.
的面积即可.
(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
∵∠AOB=∠DAO+∠ADO=2∠OAD,
∴∠DAO=∠ADO,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,![]()
∴BD=AC=10,
∵![]() ,
,
∴设AB=3x,则AD=4x,
∴(3x)2+(4x)2=102,
解得x=2或x=-2(舍去)
∴AB=6,AD=8
∴S△ABO=![]() S△ABD=
S△ABD=![]() ×
×![]() ×6×8=12.
×6×8=12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
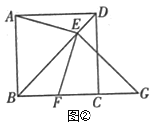
【题目】在菱形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,点
上一点,点![]() 在直线
在直线![]() 上,且
上,且![]() .如图①,当
.如图①,当![]() 时,点
时,点![]() 在线段
在线段![]() 的延长线上,线段
的延长线上,线段![]() 之间的数量关系是
之间的数量关系是![]() (无需证明);
(无需证明);

(1)如图②,当![]() ,点
,点![]() 在线段
在线段![]() 上时,线段
上时,线段![]() 之间有怎样的数量关系?写出你的猜想,并给予证明;
之间有怎样的数量关系?写出你的猜想,并给予证明;
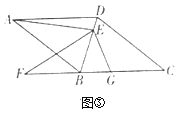
(2)如图③,当![]() ,点
,点![]() 在线段
在线段![]() 的延长线上时,直接写出线段
的延长线上时,直接写出线段![]() 之间又有怎样的数量关系?
之间又有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P显AD上一点,连接CP.
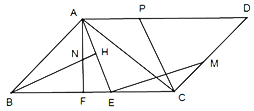
(1)若DP=2AP=4,CP=![]() ,CD=5,求△ACD的面积.
,CD=5,求△ACD的面积.
(2)若AE=BN,AN=CE,求证:AD=![]() CM+2CE.
CM+2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
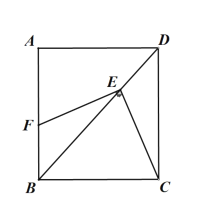
【题目】如图,已知矩形![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,连结
上一点,连结![]() ,作
,作![]() ,交
,交![]() 于
于![]() ,
,
(1)若![]() ,
,![]() 则
则![]() ________________.
________________.
(2)连结![]() 若
若![]() ,则
,则![]() ________________.
________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在去年的体育中考中,某校6名学生的体育成绩统计如下表:
成绩 | 17 | 18 | 20 |
人数 | 2 | 3 | 1 |
则下列关于这组数据的说法错误的是( )
A.众数是18B.中位数是18C.平均数是18D.方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
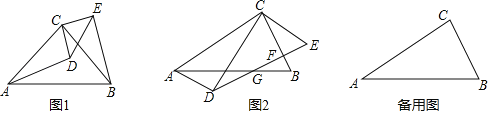
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,弦
中,弦![]() ,连接
,连接![]() 、
、![]() ;
;
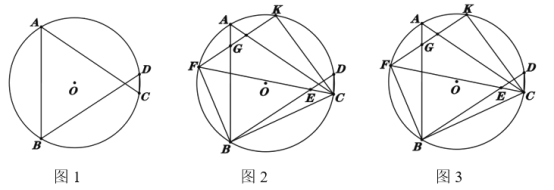
(1)如图1,求证:![]() ;
;
(2)如图2,在线段![]() 上取点
上取点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() ,求
,求![]() 的正切值;
的正切值;
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com