
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

【答案】![]()
【解析】
如图,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,设A(a,﹣![]() ),C(b,
),C(b,![]() ),根据△ABF≌△COE可得B(a+b,﹣
),根据△ABF≌△COE可得B(a+b,﹣![]() ),即(a+b)(﹣
),即(a+b)(﹣![]() )=﹣3,设
)=﹣3,设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,求得
=2,求得![]() =
=![]() ,
,![]() ,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
解:如图,连接AC,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,

易证△ABF≌△COE,设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
∵B点在在双曲线y=![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,
=2,
解得m=![]() ,或m=
,或m=![]() (舍去),
(舍去),
∴![]() =
=![]() ,
,![]() ,
,
∴S□OABC=2×S△OAC
=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×∣﹣3∣﹣
×∣﹣3∣﹣![]() ×2]
×2]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=![]() .
.
故答案为:![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
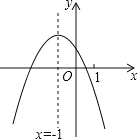
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的切线,
的切线,![]() 于点
于点![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,
,![]() ,
,
①求![]() 的度数;
的度数;
②若![]() 的半径为2,求线段
的半径为2,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计某地区供暖期间空气质量情况,某同学在20天里做了如下记录:
污染指数(ω) | 40 | 60 | 80 | 100 | 120 | 140 |
天数(天) | 3 | 2 | 3 | 4 | 5 | 3 |
其中ω<50时空气质量为优,50≤ω≤100时空气质量为良,100<ω≤150时空气质量为轻度污染.若按供暖期125天计算,请你估计该地区在供暖期间空气质量达到良以上(含良)的天数为( )
A.75B.65C.85D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有六个完全相同的小球,小球上分别标有1,2,5,7,8,13六个数,搅匀后一次从中摸出一个小球,将小球上的数记为m,则使得一次函数y=(﹣m+1)x+11﹣m经过一、二、四象限且关于x的分式方程![]() =3x+
=3x+![]() 的解为整数的概率是( )
的解为整数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com