
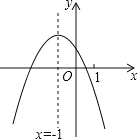
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
【答案】B
【解析】
解:∵抛物线和x轴有两个交点,
∴b2﹣4ac>0,
∴4ac﹣b2<0,∴①正确;
∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,
∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,
∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,
∴4a+c>2b,∴②错误;
∵把(1,0)代入抛物线得:y=a+b+c<0,
∴2a+2b+2c<0,
∵b=2a,
∴3b,2c<0,∴③正确;
∵抛物线的对称轴是直线x=﹣1,
∴y=a﹣b+c的值最大,
即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,
∴am2+bm+b<a,
即m(am+b)+b<a,∴④正确;
即正确的有3个,
故选B.


科目:初中数学 来源: 题型:
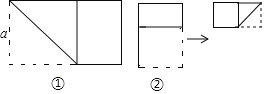
【题目】将长为2、宽为a(a大于1且小于2)的长方形纸片按如图①所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作:再把剩下的长方形按如图②所示的方式折叠并压平,剪下个边长等于此时长方形宽的正方形,称为第二次操作:如此反复操作下去…,若在第n次操作后,剩下的长方形恰为正方形,则操作终止当n=3时,a的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节木龙头50天的日用水量,得到频数分布表如下:
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后,日用水量小于0.3 m3的概率;
(2)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在范围的组中值作代表.)
查看答案和解析>>
科目:初中数学 来源: 题型:
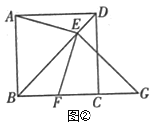
【题目】在菱形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,点
上一点,点![]() 在直线
在直线![]() 上,且
上,且![]() .如图①,当
.如图①,当![]() 时,点
时,点![]() 在线段
在线段![]() 的延长线上,线段
的延长线上,线段![]() 之间的数量关系是
之间的数量关系是![]() (无需证明);
(无需证明);

(1)如图②,当![]() ,点
,点![]() 在线段
在线段![]() 上时,线段
上时,线段![]() 之间有怎样的数量关系?写出你的猜想,并给予证明;
之间有怎样的数量关系?写出你的猜想,并给予证明;
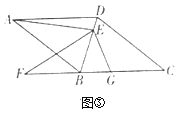
(2)如图③,当![]() ,点
,点![]() 在线段
在线段![]() 的延长线上时,直接写出线段
的延长线上时,直接写出线段![]() 之间又有怎样的数量关系?
之间又有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
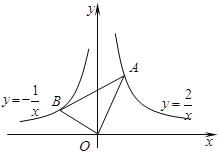
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com