
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
【答案】(1)一件产品的利润不可能是12万元.(2)不存在某个月既无盈利也不亏损.(3)![]() 或11.
或11.
【解析】
(1)设y=a+![]() ,将表中相关数据代入可求得a、b,根据12=18-(6+
,将表中相关数据代入可求得a、b,根据12=18-(6+![]() ),则
),则![]() =0可作出判断;
=0可作出判断;
(2)将n=1、x=120代入x=2n2-2kn+9(k+3)可求得k的值,先由18=6+![]() 求得x=50,根据50=2n2-26n+144可判断;
求得x=50,根据50=2n2-26n+144可判断;
(3)第m个月的利润W=x(18-y)=18x-x(6+![]() )=24(m2-13m+47),第(m+1)个月的利润为W′=24[(m+1)2-13(m+1)+47]=24(m2-11m+35),分情况作差结合m的范围,由一次函数性质可得.
)=24(m2-13m+47),第(m+1)个月的利润为W′=24[(m+1)2-13(m+1)+47]=24(m2-11m+35),分情况作差结合m的范围,由一次函数性质可得.
解 (1)由题意设![]() ,
,
由表中数据,得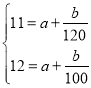 ,
,
解得![]() ,
,
则![]() .
.
由题意,若![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
∴一件产品的利润不可能是12万元.
(2)将![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() (将
(将![]() ,
,![]() 代入亦可),
代入亦可),
∴![]() .
.
由题意设![]() ,求得
,求得![]() ,
,
∴![]() ,
,
即![]() .
.
∵![]() ,
,
∴方程无实数根,
∴不存在某个月既无盈利也不亏损.
(3)设第![]() 个月的利润为
个月的利润为![]() ,
,
则![]()
![]() ,
,
∴第![]() 个月的利润为
个月的利润为![]()
![]() .
.
若![]() ,
,
则![]() ,
,![]() 取最小值1,
取最小值1,![]() 取得最大值240;
取得最大值240;
若![]() ,则
,则![]() ,
,
由![]() 知
知![]() 取最大值11,
取最大值11,![]() 取得最大值240.
取得最大值240.
∴![]() 或11.
或11.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
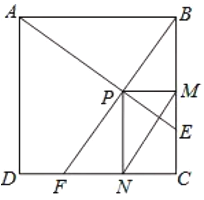
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,动点
中,动点![]() 分别以相同的速度从
分别以相同的速度从![]() 两点同时出发向点
两点同时出发向点![]() 和点
和点![]() 运动(任何一个点到达即停止),连接
运动(任何一个点到达即停止),连接![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
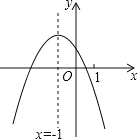
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计某地区供暖期间空气质量情况,某同学在20天里做了如下记录:
污染指数(ω) | 40 | 60 | 80 | 100 | 120 | 140 |
天数(天) | 3 | 2 | 3 | 4 | 5 | 3 |
其中ω<50时空气质量为优,50≤ω≤100时空气质量为良,100<ω≤150时空气质量为轻度污染.若按供暖期125天计算,请你估计该地区在供暖期间空气质量达到良以上(含良)的天数为( )
A.75B.65C.85D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com