
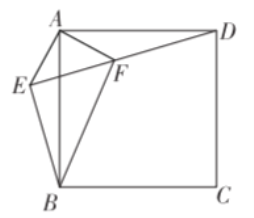
【题目】如图,![]() 是正方形
是正方形![]() 外一点,连接
外一点,连接![]() 交
交 ![]() 于点
于点![]() ,若
,若![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③ 四边形
;③ 四边形![]() 的面积是
的面积是![]() ;④点
;④点![]() 到 直线
到 直线![]() 的距离为
的距离为![]() ;⑤
;⑤![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.![]() B.2C.3D.4
B.2C.3D.4
【答案】C
【解析】
①易知AE=AF,AB=AD,所以只需证明∠EAB=∠FAD即可用SAS说明△AFD≌△AEB;
②易知∠AEB=∠AFD=135°,则∠BEF=∠AEB-∠AEF=135°-45°=90°,所以EB⊥ED;
③运用勾股定理求出EF和BE的长,根据三角形面积计算公式得出△AEF和△BEF的面积即可得到结论,
④在Rt△BEP中利用勾股定理求出![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,得等腰直角三角形
,得等腰直角三角形![]() ,根据勾股定理求得点
,根据勾股定理求得点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;则④错误;
;则④错误;
⑤在△AEB中,∠AEB=135°,AE=2,BE=![]() ,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可
,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°.
∴∠DAF+∠BAF=90°.
又∠EAB+∠BAF=90°,
∴∠EAB=∠DAF.
又AE=AF,
∴△AFD≌△AEB(SAS).
所以①正确;
∵AE=AF,∠EAF=90°,
∴∠AFE=∠AEF=45°,
∴∠AFD=180°-45°=135°.
∵△AFD≌△AEB,
∴∠AEB=∠AFD=135°,
∴∠BEF=135°-45°=90°,
即EB⊥ED,②正确;
在Rt△AEF中,∠EAF=90°,![]()
由勾股定理得,![]()
在Rt△BEF中,∠BEF=90°,
![]() ,
,![]()
![]()
![]() 四边形
四边形![]() 的面积=S△AEF+S△BEF=
的面积=S△AEF+S△BEF=![]() =
=![]() ,结论 ③ 错误;
,结论 ③ 错误;
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
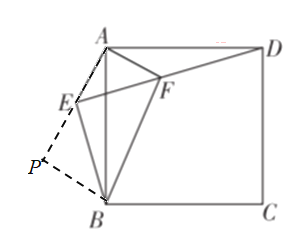
∵∠AEF=45°,∠BEF=90°
∴∠PEB=45°
∴△BPE是等腰直角三角形,
∵斜边![]() .
.
∴BP=![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() .结论 ④ 错误;
.结论 ④ 错误;
如图所示,过点A作AH⊥BE交BE延长线于H点.
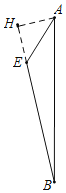
∵∠AEB=135°
∴∠AEH=45°
∴Rt△AHE是等腰三角形,
在等腰Rt△AHE中,可得AH=HE=![]() AE=
AE=![]() .
.
所以BH=![]() .
.
在Rt△AHB中利用勾股定理可得AB2=BH2+AH2,
即AB2=(![]() )2+(
)2+(![]() )2=
)2=![]() ,
,
所以⑤正确.
所以只有①、②和⑤的结论正确.
故选:C.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
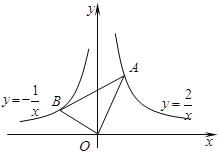
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P显AD上一点,连接CP.
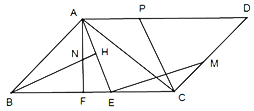
(1)若DP=2AP=4,CP=![]() ,CD=5,求△ACD的面积.
,CD=5,求△ACD的面积.
(2)若AE=BN,AN=CE,求证:AD=![]() CM+2CE.
CM+2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在去年的体育中考中,某校6名学生的体育成绩统计如下表:
成绩 | 17 | 18 | 20 |
人数 | 2 | 3 | 1 |
则下列关于这组数据的说法错误的是( )
A.众数是18B.中位数是18C.平均数是18D.方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵![]() 元,用
元,用![]() 元购进乙书包的个数与用
元购进乙书包的个数与用![]() 元购进甲书包的个数相等.
元购进甲书包的个数相等.
(1)求甲、乙两种书包的进价分别为多少元?
(2)商户购进甲、乙两种书包共![]() 个进行试销,其中甲书包的个数不少于
个进行试销,其中甲书包的个数不少于![]() 个,且甲书包的个数 的
个,且甲书包的个数 的![]() 倍不大于乙书包的个数,已知甲书包的售价为
倍不大于乙书包的个数,已知甲书包的售价为![]() 元/个,乙书包的售价为
元/个,乙书包的售价为![]() 元/个,且 全部售出,设购进甲书包
元/个,且 全部售出,设购进甲书包![]() 个,求该商店销售这批书包的利润
个,求该商店销售这批书包的利润![]() 与
与![]() 之间的函数关系式,并 写出
之间的函数关系式,并 写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,该店将![]() 个书包全部售出后,使用所获的利润又购进
个书包全部售出后,使用所获的利润又购进![]() 个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利
个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利![]() 元.请求出该店第二次进货所选用的进货方案?
元.请求出该店第二次进货所选用的进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
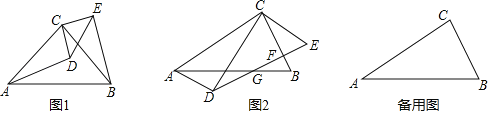
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
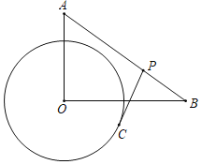
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PC(点C为切点),则线段PC长的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com