
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,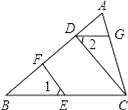
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.
【答案】
(1)
解:DG∥BC,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF,
∴∠1=∠BCD,
∵∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC
(2)
解:∵∠A=70°,∠B=40°,
∴∠ACB=180°﹣∠B﹣∠A=70°,
∵DG∥BC,
∴∠AGD=∠ACB=70°
【解析】(1)根据平行线的判定推出CD∥EF,根据平行线的性质得出∠1=∠BCD,求出∠2=∠BCD,根据平行线的判定得出即可;(2)根据三角形内角和定理求出∠ACB,根据平行线的性质得出∠AGD=∠ACB,即可得出答案.
【考点精析】本题主要考查了平行线的判定和平行线的判定与性质的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点E是ABCD中BC边的中点,若∠ABE=∠BAE=60°,BC=4,连接AE并延长交DC的延长线于点F. 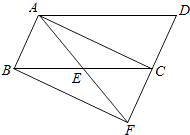
(1)连接AC,BF,求证:四边形ABFC为矩形;
(2)求四边形ABFC的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 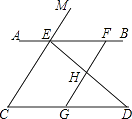
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是2018年10月份的日历,在日历上任意圈出一个竖列相邻的3个数,如果被圈出的3个数之和为54,那么这3个数中最后一天为2018年 10月( )
一 | 二 | 三 | 四 | 五 | 六 | 日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
22 | 23 | 24 | 25 | 26 | 27 | 28 |
29 | 30 | 31 |
A. 19号 B. 25号 C. 21号 D. 31号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程 2x 2 - x + 1 = 0的根的情况是( )
A. 有一个实数根B. 有两个不相等的实数根
C. 没有实数根D. 有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年,我国网络购物市场交易规模达61000亿元,较2016年增长29.6%.61000亿用科学记数法表示为( )
A. 6.1×1012B. 6.1×1011C. 6.1×108D. 6.1×104
查看答案和解析>>
科目:初中数学 来源: 题型:
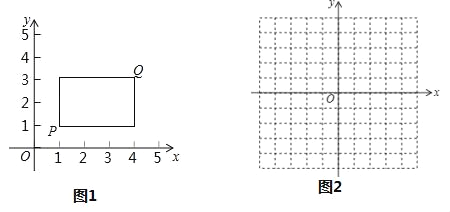
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)正方形RSKT顶点R的坐标为(-1,1),K的坐标为(2,-2),点M的坐标为(m,3),若在正方形RSKT边上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( ) 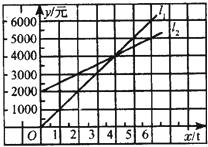
A.小于3t
B.大于3t
C.小于4t
D.大于4t
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com