
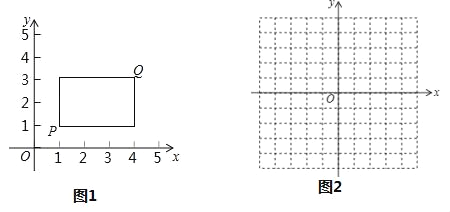
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ�����ͼΪ��P��Q�ġ���ؾ��Ρ�ʾ��ͼ��
��1����֪��A������Ϊ��1��0����
������B������Ϊ��3��1�������A��B�ġ���ؾ��Ρ��������
�ڵ�C��ֱ��x=3�ϣ�����A��C�ġ���ؾ��Ρ�Ϊ�����Σ���ֱ��AC�ı���ʽ��
��2��������RSKT����R������Ϊ��-1��1����K������Ϊ��2��-2������M������Ϊ��m��3��������������RSKT���ϴ���һ��N��ʹ�õ�M��N�ġ���ؾ��Ρ�Ϊ�����Σ���m��ȡֵ��Χ��
���𰸡���1����2����y=x��1��y=��x+1����2��1��m��7��0��m��6
�����������������
��1��������ؾ��εĶ����֪��Ҫ��A��B����ؾ����������AB��Ϊ�Խ��ߣ�����A��B��������꼴������þ��εĵ���ߵij��ȣ�����������þ��ε������
���ɶ����֪��AC��Ϊ�����εĶԽ��ߣ�����AC��x��ļнDZ�Ϊ45�㣬��ֱ��AC�Ľ���ʽΪ��y=kx+b���ɴ˿�֪k=��1���٣�1��0������y=kx+b���������b��ֵ��
��2���ɶ����֪��MN��Ϊ��ؾ��εĶԽ��ߣ�������ؾ��ε�Ϊ�����Σ���ֱ��MN��x��ļн�Ϊ45�㣬����ֱ��ƽ�п������m�ķ�Χ��
�����������1���١�A��1��0����B��3��1��
�ɶ����֪����A��B������ؾ������ĵ���߷ֱ�Ϊ2��1��
���A��B������ؾ����������Ϊ2��1=2��
���ɶ����֪��AC�ǵ�A��C������ؾ������ĶԽ��ߣ�
�֡ߵ�A��C������ؾ�����Ϊ������
��ֱ��AC��x��ļн�Ϊ45����
��ֱ��AC�Ľ���Ϊ��y=x+m��y=��x+n
�ѣ�1��0���ֱ�y=x+m��
��m=��1��
��ֱ��AC�Ľ���Ϊ��y=x��1��
�ѣ�1��0������y=��x+n��
��n=1��
��y=��x+1��
��������������A��C������ؾ�����Ϊ�����Σ�ֱ��AC�ı���ʽΪy=x��1��y=��x+1��
��2����ֱ��MN�Ľ���ʽΪy=kx+b��
�ߵ�M��N������ؾ�����Ϊ�����Σ�
���ɶ����֪��ֱ��MN��x��ļн�Ϊ45����
��k=��1��
�ߵ�N�������α��ϣ�
�൱ֱ��MN���������н���ʱ����M��N������ؾ�����Ϊ�����Σ�
��k=1ʱ��
����R��K��ֱ����ֱ��MNƽ�У�
����-1,1���ͣ�2��-2���ֱ����y=x+b
��b=2 ��b=-4
��M��m��3������y=x+2��y=x-4��
��m=1 m=7
��1��m��7��
��k=��1ʱ����(-1,-2) (2,1)����y=��x+b��
��b=-3 b=3��
��M��m��3������y=-x-3��y=-x+3��
��m=0 m=6
��0��m��6��
��������������M��N������ؾ�����Ϊ������ʱ��m��ȡֵ��Χ�ǣ�1��m��7��0��m��6



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD��AB��EF��AB������ֱ�ΪD��F����1=��2��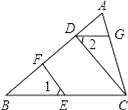
��1�����ж�DG��BC��λ�ù�ϵ����˵�����ɣ�
��2������A=70�㣬��B=40�㣬���AGD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���B=��D=90�㣬AE��CF�ֱ�ƽ�֡�BAD�͡�BCD������ֱ��AE��CF��λ�ù�ϵ��Σ���˵��������ɣ� 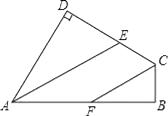
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֽ���ʽ��16��x2=��������
A.��4��x����4+x��
B.��x��4����x+4��
C.��8+x����8��x��
D.��4��x��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�̵���ijʱ����ÿ��480Ԫ�ļ۸����������·�������һ��ӯ��20%����һ������20%�����������·���ӯ�����ǿ��𣬻��Dz�ӯ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���B=��D=90�㣬AE��CF�ֱ�ƽ�֡�BAD�͡�BCD������ֱ��AE��CF��λ�ù�ϵ��Σ���˵��������ɣ� 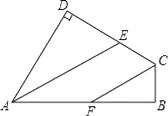
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������뻯��
��1��12������6��+����9��
��2������1��2016+����4��2�£��� ![]() ��+|��1��2|
��+|��1��2|
��3���Ȼ�������ֵ���� ![]() ��4a2+2a��2��+��a��1��������a=
��4a2+2a��2��+��a��1��������a= ![]()
��4����P�������ϵ�λ����ͼ��ʾ������|p��1|+|p��2| ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʱ��Ҫ�����ѡ���˫���ϸǵij�����ֽ���װ���ϸ�ֽ������պõ��ڵ��������2��������ͼ
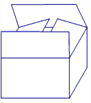
(1)ʵ�����ã����Ҫ��ֽ��ĸ�Ϊ0.5�ף������ǻƽ���Σ����볤�ı��ǻƽ�ȣ� ȡ�ƽ��Ϊ0.6�������Ϊ0.3�����ף�
�ٰ�����1����ͼ����һ��ֽ�䣬��Ҫ����Ӳֽ��A1B1C1D1������Ƕ���ƽ���ף�
��С����Ϊ������ӽ�ʡ���ϵĽǶȿ��ǣ����÷���2����ͼ��������Ӳֽ��A2B2C2D2 ��һ��ֽ��ȷ���1���ţ�����Ϊ�أ���˵�����ɣ�
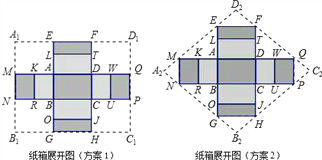
��2����չ˼ά��ˮ���̴����ڲ��ع���һ�������ѡ��������о���1���е�ֽ�����̫���˳�����Ҫ��ֽ��ĵ����ܳ�����������߶����Ϊԭ����һ�룬����Ϊˮ���̵�Ҫ���ܰ쵽�������ú���ͼ����֤��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com