
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 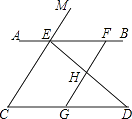
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
【答案】
(1)证明:∵∠CED=∠GHD,
∴CE∥GF;
(2)解:∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°
(3)解:∵∠DHG=∠EHF=100°,∠D=30°,
∴∠CGF=100°+30°=130°,
∵CE∥GF,
∴∠C=180°﹣130°=50°,
∵AB∥CD,
∴∠AEC=50°,
∴∠AEM=180°﹣50°=130°
【解析】(1)根据同位角相等两直线平行,可证CE∥GF;(2)根据平行线的性质可得∠C=∠FGD,根据等量关系可得∠FGD=∠EFG,根据内错角相等,两直线平行可得AB∥CD,再根据平行线的性质可得∠AED与∠D之间的数量关系;(3)根据对顶角相等可求∠DHG,根据三角形外角的性质可求∠CGF,根据平行线的性质可得∠C,∠AEC,再根据平角的定义可求∠AEM的度数.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】四边形的四边顺次为a、b、c、d,且满足a2+b2+c2+d2=2(ab+cd),则这个四边形一定是( )
A.平行四边形
B.两组对角分别相等的四边形
C.对角线互相垂直的四边形
D.对角线长相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b=![]() (m2﹣1)和c=
(m2﹣1)和c=![]() (m2+1)是勾股数.
(m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
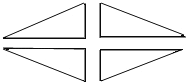
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm;三角形中至少有一边上的高为8 cm,
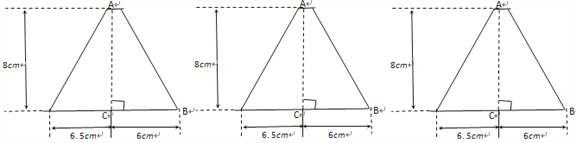
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城是一让人打开心扉的城市,吸引了很多的国内外游客,春风旅行社对3月份本社接待的外地游客来盐城旅游的首选景点作了一次抽样调查. 调查结果如下图表:

(1)此次共调查了多少人?
(2)请将以上图表补充完整.
(3)该旅行社预计4月份接待外地来杭的游客2500人,请你估计首选去丹顶鹤的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,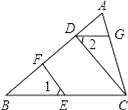
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)12﹣(﹣6)+(﹣9)
(2)(﹣1)2016+(﹣4)2÷(﹣ ![]() )+|﹣1﹣2|
)+|﹣1﹣2|
(3)先化简,再求值:﹣ ![]() (4a2+2a﹣2)+(a﹣1),其中a=
(4a2+2a﹣2)+(a﹣1),其中a= ![]()
(4)点P在数轴上的位置如图所示,化简:|p﹣1|+|p﹣2| ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com