
【题目】已知:△ABC(如图),
(1)求作:作△ABC的内切圆⊙I.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明).
(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
【答案】(1)作图见解析;(2)134°.
【解析】
试题(1)分别作出∠BAC、∠ABC的平分线,两平分线的交点即为△ABC的内切圆的圆心I,过点I向BC作垂线,垂足为H,垂足与I之间的距离即为⊙I的半径,以I为圆心,IH为半径画圆即可;
(2)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的性质得出∠IBC+∠ICB的度数,由三角形内角和定理即可求解.
试题解析:(1)①以A为圆心任意长为半径画圆,分别交AC、AB于点H、G;
②分别以H、G为圆心,以大于![]() HG为半径画圆,两圆相交于K点,连接AK,则AK即为∠BAC的平分线;
HG为半径画圆,两圆相交于K点,连接AK,则AK即为∠BAC的平分线;
③同理作出∠ABC的平分线BF,交AK于点I,则I即为△ABC内切圆的圆心;
④过I作IH⊥BC于H,以I为圆心,IH为半径画,则⊙I即为所求圆.
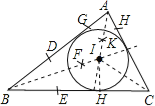
(2)∵∠BAC=88°,
∴∠ABC+∠ACB=180°-88°=92°,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×92°=46°,
×92°=46°,
∴∠BIC=180°-46°=134°.
考点: 三角形的内切圆与内心.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①
连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④MO平分
;④MO平分![]() ,正确的个数有( )
,正确的个数有( )
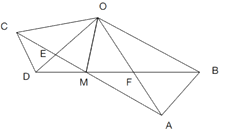
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x﹣3,点B表示的数为2x+1,点C表示的数为﹣4,若将△ABC向右滚动,则x的值等于_____,数字2012对应的点将与△ABC的顶点_____重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为( )
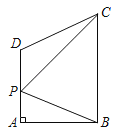
A.5B.6C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
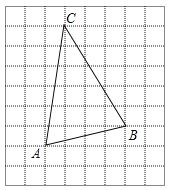
【题目】(2017天津)如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于____;
(2)在△ABC的内部有一点P,满足S△PS△PS△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示:
所抽取该校七年级学生四月份“读书量”的统计图
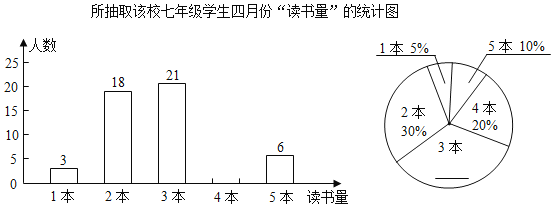
根据以上信息,解答下列问题:
(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量"的众数为____________.
(2)求本次所抽取学生四月份“读书量"的平均数.
(3)已知该校七年级有![]() 名学生,请你估计该校七年级学生中,四月份“读书量”为
名学生,请你估计该校七年级学生中,四月份“读书量”为![]() 本的学生人数.
本的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com