
【题目】如图,在![]() 和
和![]() 中,
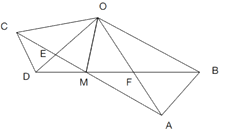
中,![]() 连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①
连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④MO平分
;④MO平分![]() ,正确的个数有( )
,正确的个数有( )
A.4个B.3个C.2个D.1个
【答案】B
【解析】
由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,①正确;
由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=30°,②正确;
作OG⊥MC于G,OH⊥MB于H,则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH,得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,④正确;
由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故③错误;即可得出结论.
解:![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,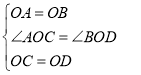 ,
,
![]() ,
,
![]() ,
,![]() ,①正确;
,①正确;
![]() ,
,
由三角形的外角性质得:![]() ,
,
![]() ,②正确;
,②正确;
作![]() 于
于![]() ,
,![]() 于
于![]() ,如图所示:
,如图所示:
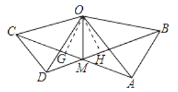
则![]() ,
,
在![]() 和
和![]() 中,
中,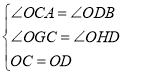 ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,④正确;
,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,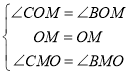 ,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB
∴OA=OC
与OA>OC矛盾,
∴③错误;
正确的个数有3个;
故选择:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知 y 与 x﹣2 成正比例,且当 x =﹣4 时, y =﹣3.
(1)求 y 与 x 的函数关系式;
(2)若点 M(5.1,m)、N(﹣3.9,n)在此函数图像上,判断 m 与 n 的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对![]() 定义一种新运算
定义一种新运算![]() ,规定:
,规定: ![]() (其中
(其中![]() 均为非零常数),这里等式右边是通常的四则运算,例如:
均为非零常数),这里等式右边是通常的四则运算,例如: ![]() .
.
(1)已知![]() .
.
①求![]() 的值:
的值:
②若关于![]() 的不等式组
的不等式组![]() 无解,求实数
无解,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 对任意实数
对任意实数![]() 都成立(这里
都成立(这里![]() 和
和![]() 均有意义),则
均有意义),则![]() 应满足怎样的关系式
应满足怎样的关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]()
![]() 若抛物线的对称轴是直线
若抛物线的对称轴是直线![]() ,求
,求![]() 的值.
的值.
![]() 若抛物线与
若抛物线与![]() 轴负半轴交于两个点,且这两点距离为
轴负半轴交于两个点,且这两点距离为![]() ,求
,求![]() 的值.
的值.
![]() 若抛物线与
若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交点为
轴交点为![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的边CD上一点,BP的垂直平分线EF分别交BC、AD于E、F两点,GP⊥EP交AD于点G,连接BG交EF于点 H,下列结论:①BP=EF;②∠FHG=45°;③以BA为半径⊙B与GP相切;④若G为AD的中点,则DP=2CP.其中正确结论的序号是( )
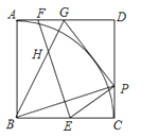
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
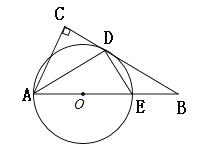
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度![]() (米)与挖掘时间
(米)与挖掘时间![]() (时)之间关系的部分图象.请解答下列问题:
(时)之间关系的部分图象.请解答下列问题:
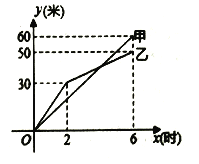
![]() 在前
在前![]() 小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
![]() ①当
①当![]() 时,求出
时,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②开挖几小时后,两工程队挖掘隧道长度相差![]() 米?
米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC(如图),
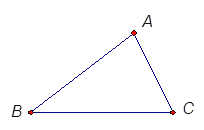
(1)求作:作△ABC的内切圆⊙I.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明).
(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com