
 22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由.
22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为
小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为| 6 |
| 6 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
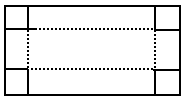
如图所示,有一块矩形的铁片,在它的四个角上各自剪去一个边长是4cm的小正方形,然后把四边折起来,恰好做成一个没盖的盒子,已知铁片的长是宽的2倍,做成的盒子的容积是1536 ,求这块铁片的长和宽.
,求这块铁片的长和宽.

查看答案和解析>>
科目:初中数学 来源: 题型:044
如图所示,有一块矩形的铁片,在它的四个角上各自剪去一个边长是4cm的小正方形,然后把四边折起来,恰好做成一个没盖的盒子,已知铁片的长是宽的2倍,做成的盒子的容积是1536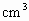 ,求这块铁片的长和宽.
,求这块铁片的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
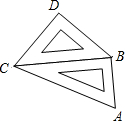 小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为________.
小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为________.查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知抛物线![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在该抛物线图象上,且以
在该抛物线图象上,且以![]() 为直径的⊙
为直径的⊙![]() 恰好经过顶点
恰好经过顶点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 的纵坐标为
的纵坐标为![]() ,且点
,且点![]() 在该抛物线的对称轴
在该抛物线的对称轴![]() 上运动,试探索:
上运动,试探索:
①当![]() 时,求
时,求![]() 的取值范围(其中:
的取值范围(其中:![]() 为△
为△![]() 的面积,
的面积,![]() 为△
为△![]() 的面积,
的面积,![]() 为四边
为四边
形OACB的面积);
②当![]() 取何值时,点
取何值时,点![]() 在⊙
在⊙![]() 上.(写出
上.(写出![]() 的值即可)
的值即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com