
【题目】如图,在△ABC中,AB=AC,AD是中线,且AC是DE的中垂线.
(1)求证:∠BAD=∠CAD;
(2)连接CE,写出BD和CE的数量关系.并说明理由;
(3)当∠BAC=90°,BC=8时,在AD上找一点P,使得点P到点C与到点E的距离之和最小,并求出此时△BCP的面积.
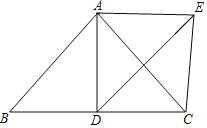
【答案】(1)详见解析;(2)BD=CE,理由详见解析;(3)8
【解析】
(1)根据等腰三角形的性质即可得到结论;
(2)根据AC垂直平分DE,可得CD=CE,又BD=CD即可证明;
(3)连接BE交AD于点P,此时PE+PC的值最小.先求出AD的长,再证明△APE≌△DPB,得出PA=PD,求出PD即可得出△BCP的面积.
(1)证明:∵AB=AC,AD是中线,
∴∠BAD=∠CAD;
(2)解:BD=CE.理由如下:
∵AD是中线,∴BD=CD,
∵AC垂直平分DE,∴CD=CE,
∴BD=CE;
(3)解:连接BE,BE与AD的交点即为点P,
∵AB=AC,D为BC的中点,∴AD⊥BC,即AD垂直平分BC,
∴BP=CP,
∴PE+PC=PE+BP=BE,所以此时PE+PC的值最小.
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,∴∠ABC=∠ACB=45°=∠DAC=∠BAD,
∴AD=BD=CD=4,
由AC垂直平分DE得,AE=AD=BD,
∴∠ADE=90°-∠DAC=45°=∠AED,
∴∠DAE=90°,
∴∠PAE=∠BDP=90°,
又∠BPD=∠EPA,
∴△APE≌△DPB(AAS),
∴PA=PD=2,
∵PD⊥BC,
∴S△BCP=![]() ×8×2=8.
×8×2=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
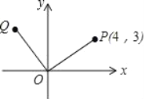
【题目】如图,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 ;
(2)若把点Q向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q′恰好落在第三象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG 于点E,CF⊥AG于点F,则AE-GF的值为( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
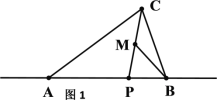
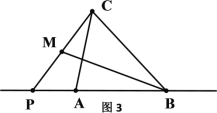
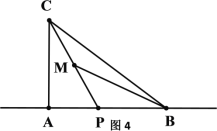
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
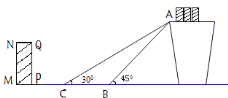
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com