
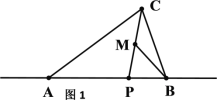
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
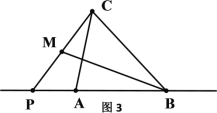
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
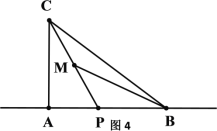
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

【答案】(1)真;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据直角三角形斜边的中线等于斜边的一半可知MP=MB,从而∠MPB=∠MBP,然后根据三角形外角的性质说明即可;
(2)先证明△PAC∽△PMB,然后根据相似三角形的性质求解即可;
(3)分三种情况求解:P为线段AB上的“好点”, P为线段AB延长线上的“好点”, P为线段BA延长线上的“好点”.
(1)真 .
理由如下:如图,当∠ABC=90°时,M为PC中点,BM=PM,
则∠MPB=∠MBP>∠ACP,
所以在线段AB上不存在“好点”;
(2)∵P为BA延长线上一个“好点”;
∴∠ACP=∠MBP;
∴△PAC∽△PMB;
∴![]() 即
即![]() ;
;
∵M为PC中点,
∴MP=2;
∴![]() ;
;
∴![]() .
.
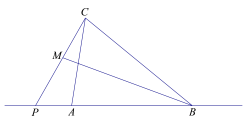
(3)第一种情况,P为线段AB上的“好点”,则∠ACP=∠MBA,找AP中点D,连结MD;
∵M为CP中点;
∴MD为△CPA中位线;
∴MD=2,MD//CA;
∴∠DMP=∠ACP=∠MBA;
∴△DMP∽△DBM;
∴DM2=DP·DB即4= DP·(5![]() DP);
DP);
解得DP=1,DP=4(不在AB边上,舍去;)
∴AP=2
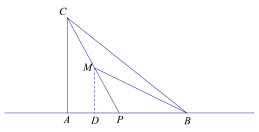
第二种情况(1),P为线段AB延长线上的“好点”,则∠ACP=∠MBA,找AP中点D,此时,D在线段AB上,如图,连结MD;
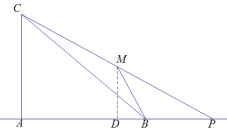
∵M为CP中点;
∴MD为△CPA中位线;
∴MD=2,MD//CA;
∴∠DMP=∠ACP=∠MBA;
∴△DMP∽△DBM
∴DM2=DP·DB即4= DP·(5![]() DA)= DP·(5
DA)= DP·(5![]() DP);
DP);
解得DP=1(不在AB延长线上,舍去),DP=4
∴AP=8;
第二种情况(2),P为线段AB延长线上的“好点”,找AP中点D,此时,D
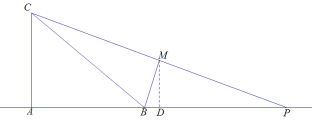
此时,∠MBA>∠MDB>∠DMP=∠ACP,则这种情况不存在,舍去;

第三种情况,P为线段BA延长线上的“好点”,则∠ACP=∠MBA,
∴△PAC∽△PMB;
∴![]()
∴BM垂直平分PC则BC=BP=![]() ;
;
∴![]()
∴综上所述,![]() 或
或![]() 或
或![]() ;
;


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
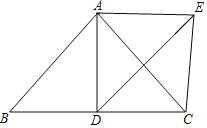
【题目】如图,在△ABC中,AB=AC,AD是中线,且AC是DE的中垂线.
(1)求证:∠BAD=∠CAD;
(2)连接CE,写出BD和CE的数量关系.并说明理由;
(3)当∠BAC=90°,BC=8时,在AD上找一点P,使得点P到点C与到点E的距离之和最小,并求出此时△BCP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
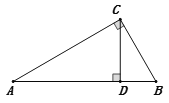
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,△BCD的周长为(6+2![]() )cm,则△ABC的周长为( )cm.
)cm,则△ABC的周长为( )cm.
A.(9+2![]() )B.(12+
)B.(12+![]() )C.(12+4
)C.(12+4![]() )D.(18+2
)D.(18+2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
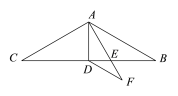
【题目】如图:在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为___________;
查看答案和解析>>
科目:初中数学 来源: 题型:
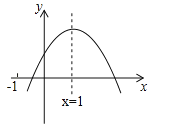
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①abc>0,
②a﹣b+c<0,
③2a=b,
④4a+2b+c>0,
⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .
.
其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
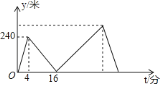
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com