
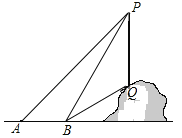
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为45°,然后他沿着正对树PQ的方向前进10m到达点B处,此时测得树顶P和树底Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求树PQ的高度.
【答案】(1)30°;(2)10+![]() .
.
【解析】
(1)延长PQ交直线AB于点C,根据直角三角形两锐角互余求得即可;
(2)设PC=x,在直角△APC和直角△BPC中,根据三角函数利用x表示出AC和BC,根据AB=AC﹣BC即可列出方程求得x的值,再在直角△BQC中利用三角函数求得QC的长,则PQ的长度即可求解.
延长PQ交直线AB于点C,(1)∠BPQ=90°﹣60°=30°;
(2)设PC=x.在直角△APC中,∠PAC=45°,则AC=PC=x;
∵∠PBC=60°,∴∠BPC=30°.
在直角△BPC中,BC![]() PC
PC![]() x.
x.
∵AB=AC﹣BC=10,∴x![]() x=10,解得:x=15+5
x=10,解得:x=15+5![]() .
.
则BC=5![]() 5.
5.
在直角△BCQ中,QC![]() BC
BC![]() (5
(5![]() 5)=5
5)=5![]() ,∴PQ=PC﹣QC=15+5
,∴PQ=PC﹣QC=15+5![]() (5
(5![]() )=10
)=10![]() .
.
答:树PQ的高度为(10![]() )m.
)m.


科目:初中数学 来源: 题型:
【题目】如图,点P为正方形ABCD的边CD上一点,BP的垂直平分线EF分别交BC、AD于E、F两点,GP⊥EP交AD于点G,连接BG交EF于点 H,下列结论:①BP=EF;②∠FHG=45°;③以BA为半径⊙B与GP相切;④若G为AD的中点,则DP=2CP.其中正确结论的序号是( )
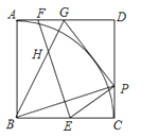
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
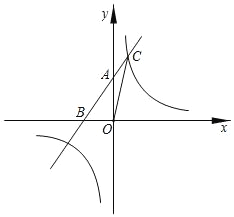
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个被平均分成![]() 等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为
等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为![]() ,乙转动转盘后指针所指区域内的数字为
,乙转动转盘后指针所指区域内的数字为![]() (当指针在边界上时,重转一次,直到指向一个区域为止).
(当指针在边界上时,重转一次,直到指向一个区域为止).

![]() 直接写出甲转动转盘后所指区域内的数字为负数的概率;
直接写出甲转动转盘后所指区域内的数字为负数的概率;
![]() 用树状图或列表法,求出点
用树状图或列表法,求出点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
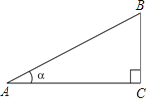
【题目】如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)ctan30°= ;
(2)如图,已知tanA=![]() ,其中∠A为锐角,试求ctanA的值.
,其中∠A为锐角,试求ctanA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
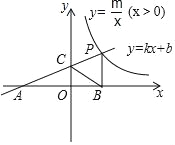
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<![]() 的x的取值范围;
的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com