
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
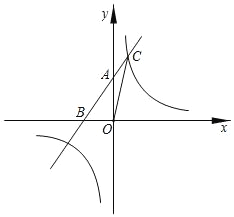
【答案】(1)y=![]() ;(2)1;(3)x<﹣3或0<x<1.
;(2)1;(3)x<﹣3或0<x<1.
【解析】
(1)将点C坐标分别代入直线y=x+2和反比例函数y=![]() ,可求点C坐标,即可求反比例函数的解析式;
,可求点C坐标,即可求反比例函数的解析式;
(2)由题意可得点A(0,2),点B(-2,0),即可求△AOC的面积;
(3)列出方程组可求直线y=x+2和反比例函数y=![]() 的交点坐标,根据图象可求不等式x+2-
的交点坐标,根据图象可求不等式x+2-![]() <0的解集.
<0的解集.
解:(1)∵点C(1,a)在直线y=x+2上,
∴a=1+2=3
∴点C(1,3)
∵点C在反比例函数y=![]() 图象上,
图象上,
∴k=1×3=3
∴反比例函数的解析式y=![]()
(2)∵直线y=x+2与坐标轴相交于A,B两点,
∴点A(0,2),点B(﹣2,0)
∴OA=2
∴S△AOC=![]() ×1×2=1
×1×2=1
(3)∵
解得:![]() ,
,![]()
∴直线y=x+2与反比例函数y=![]() 的交点为(1,3),(﹣3,﹣1)
的交点为(1,3),(﹣3,﹣1)
∴不等式x+2﹣![]() <0的解集为:x<﹣3或0<x<1.
<0的解集为:x<﹣3或0<x<1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0有两个实数根x1, x2,那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知a、b是方程x2+15x+5=0的二根,则![]() =?
=?
(2)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
(3)结合二元一次方程组的相关知识,解决问题:已知![]() 和
和![]() 是关于x,y的方程组
是关于x,y的方程组![]() 的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣
的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣![]() =2?若存在,求出的k值,若不存在,请说明理由.
=2?若存在,求出的k值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(x1,y1)、B(x2,y2)都在某函数图象上,且当x1<x2<0时,y1>y2,则此函数一定不是( )
A. ![]() B. y=﹣2x+1 C. y=x2﹣1 D.
B. y=﹣2x+1 C. y=x2﹣1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
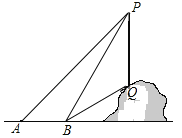
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为45°,然后他沿着正对树PQ的方向前进10m到达点B处,此时测得树顶P和树底Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求树PQ的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
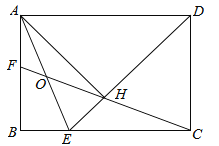
【题目】(3分)如图,在矩形ABCD中,BC=![]() AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正确命题的序号是 (填上所有正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中的点A(a,1),t=ab﹣a2﹣b2(a,b是实数)
(1)若关于x的反比例函数y=![]() 过点A,求t的取值范围.
过点A,求t的取值范围.
(2)若关于x的一次函数y=bx过点A,求t的取值范围.
(3)若关于x的二次函数y=x2+bx+b2过点A,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com