
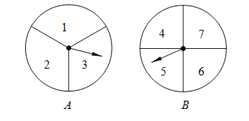
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
【答案】(1)答案见试题解析;(2)P(甲获胜)=![]() ,P(乙获胜)=
,P(乙获胜)=![]() .
.
【解析】
试题(1)列表得出所有等可能的情况数即可;
(2)找出积为奇数与积为偶数的情况数,分别求出甲乙两人获胜的概率即可.
试题解析:(1)所有可能出现的结果如图:
4 | 5 | 6 | 7 | |
1 | (1,4)4 | (1,5)5 | (1,6)6 | (1,7)7 |
2 | (2,4)8 | (2,5)10 | (2,6)12 | (2,7)14 |
3 | (3,4)12 | (3,5)15 | (3,6)18 | (3,7)21 |
(2)从上面的表格(或树状图)可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中积是奇数的结果有4种,即5、7、15、21,积是偶数的结果有8种,即4、6、8、10、12、14、12、18,∴甲、乙 两人获胜的概率分别为:P(甲获胜)=![]() =
=![]() ,P(乙获胜)=
,P(乙获胜)=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
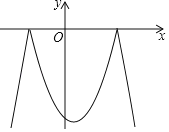
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
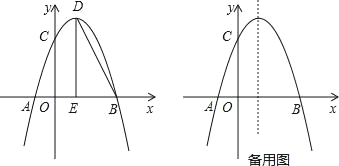
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
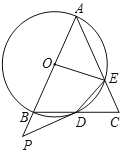
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
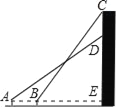
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
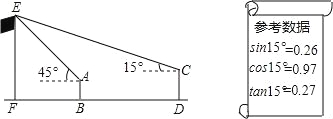
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,以OA2为斜边在△OA1A2外部作等腰直角△OA2A3,以OA3为斜边在△OA2A3外部作等腰直角△OA3A4,以OA4为斜边在△OA3A4外部作等腰直角△OA4A5,…,连接A1A3,A2A4,A3A5,…分别与OA2,OA3,OA4,交于点C1,C2,C3,按此规律继续下去,则△OAnCn的面积等于_____.(用含正整数n的式子表示)
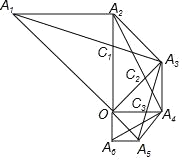
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com