
| x | -2 | 1 | 5 |
| y | m | n | p |
分析 根据a>0,抛物线开口向上,对称轴x=1左侧y随x的增大而减小,得m>n,对称轴x=1右侧y随x的增大而增大,得p>n,再由抛物线的对称性,可得出当x=-2时与x=4时的函数值相等,得p>m,从而得出m、n、p的大小关系.
解答 解:∵a>0,
∴抛物线开口向上,
∵对称轴为x=1,
∴对称轴左侧y随x的增大而减小,
∵-2<1,
∴m>n,
∵对称轴x=1右侧y随x的增大而增大,
∴p>n,
∵x=-2时与x=4时的函数值相等,
∴p>m,
∴p>m>n,
故答案为n<m<p.
点评 本题考查了二次函数图象上点的坐标特征,解题关键是:(1)找到二次函数的对称轴;(2)根据对称性将两个点移到对称轴同侧比较.


科目:初中数学 来源: 题型:选择题
| A. | a+b+c=12 | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:2:3 | D. | a2+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
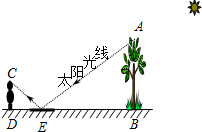 如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为6米.
如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a≥0时,$\sqrt{{a}^{2}}$=a | B. | $\root{3}{{a}^{3}}$=a | C. | 当a<0时,$\sqrt{{a}^{2}}$=-a | D. | $\sqrt{(-9)^{2}}$=-9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com