
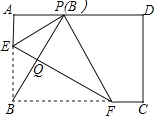
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )

A.①② B.②③ C.①③ D.①④
【答案】D
【解析】
试题分析:求出BE=2AE,根据翻折的性质可得PE=BE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠APE=30°,然后求出∠AEP=60°,再根据翻折的性质求出∠BEF=60°,根据直角三角形两锐角互余求出∠EFB=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得EF=2BE,判断出①正确;利用30°角的正切值求出PF=![]() PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③错误;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,判断出④正确.
PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③错误;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,判断出④正确.
解:∵AE=![]() AB,
AB,
∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°﹣30°=60°,
∴∠BEF=![]() (180°﹣∠AEP)=
(180°﹣∠AEP)=![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠EFB=90°﹣60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,故④正确;
综上所述,结论正确的是①④.
故选:D.


科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.

(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 有一组邻边相等的梯形是等腰梯形;
B. 一组对边平行,另一组对边相等的四边形是等腰梯形;
C. 有一组对角互补的梯形是等腰梯形;
D. 有两组对角分别相等的四边形是等腰梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快镇康经济社会发展,促进区域资源开发,巩固国防维护边境稳定,2016 年 11 月镇康县(南伞)至孟定(清水河)高速公路段可行性研究报告通过省发改委批复,预计总投资 55 亿余元,55 亿用科学记数法表示为__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星机械厂有煤80吨,每天需烧煤5吨,求工厂余煤量y(吨)与烧煤天数x(天)之间的函数表达式,指出y是不是x的一次函数,并求自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com