
【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
【答案】(1)若计划花费160元在该公园的门票上时,则选择购买C类年票进入公园的次数最多,为13次.(2)一年中进入该公园超过30次时,购买A类年票比较合算.
【解析】
(1)160元不可能选A年票,分别算出选择B、C年票的次数,比较之后进行选择即可;(2)设超过x次时,购买A类年票比较合算,依题意列出不等式组,解出不等式组即可
(1)解:不可能选A年票.若选B年票,则![]() ;
;
若选C年票,则![]() ;
;
若不购买年票,则![]()
所以,若计划花费160元在该公园的门票上时,则选择购买C类年票进入公园的次数最多,为13次.
(2)解:设超过x次时,购买A类年票比较合算,依题意得
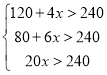
解得![]()
因此,一年中进入该公园超过30次时,购买A类年票比较合算.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() ,
,![]() 的方程组
的方程组![]() ,则下列结论中:①当
,则下列结论中:①当![]() 时,方程组的解是
时,方程组的解是![]() ;②当
;②当![]() ,
,![]() 的值互为相反数时,
的值互为相反数时,![]() ;③不存在一个实数
;③不存在一个实数![]() 使得
使得![]() ;④若
;④若![]() ,则
,则![]() 正确的个数有( )
正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
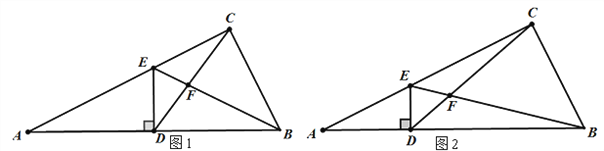
【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=![]() ,则
,则![]() =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若![]() ,tanA=
,tanA=![]() ,则
,则![]() =____.
=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 的解析式是
的解析式是![]() ,并且与
,并且与![]() 轴、
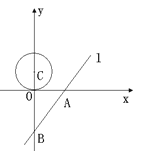
轴、![]() 轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着
轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着![]() 轴向下运动,当⊙C与直线
轴向下运动,当⊙C与直线![]() 相切时,则该圆运动的时间为( )
相切时,则该圆运动的时间为( )
A. 3秒或6秒 B. 6秒 C. 3秒 D. 6秒或16秒
查看答案和解析>>
科目:初中数学 来源: 题型:
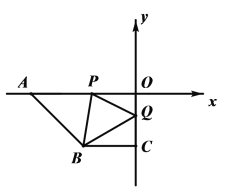
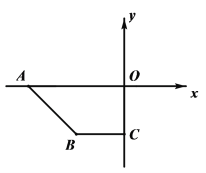
【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足![]() ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使![]() ,求出点P的坐标;
,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0),B(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(提示:平行四边形的面积=底×高)
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
的值是否发生变化,若不变请求出该值,若会变请并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)分解因式:
①x2-8xy+16y2
②(x+y+1)2-(x-y+1)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com