
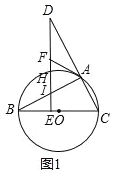
【题目】如图1,BC是![]() 的直径,点A在
的直径,点A在![]() 上,点D在CA的延长线上,
上,点D在CA的延长线上,![]() ,垂足为点E,DE与
,垂足为点E,DE与![]() 相交于点H,与AB相交于点
相交于点H,与AB相交于点![]() 过点A作
过点A作![]() ,与DE相交于点F.
,与DE相交于点F.
![]() 求证:AF为
求证:AF为![]() 的切线;
的切线;
![]() 当
当![]() ,且
,且![]() 时,求:
时,求:![]() 的值;
的值;
![]() 如图2,在
如图2,在![]() 的条件下,延长FA,BC相交于点G,若
的条件下,延长FA,BC相交于点G,若![]() ,求线段EH的长.
,求线段EH的长.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一客车一出租车分别从甲乙两地相向而行同时出发,设客车离甲地距离为y1千米,出租车离甲地距离为y2千米,两车行驶的时间为x小时,y1、y2关于的函数图象如图所示:

(1)根据图象,直接写出y1、y2关于x的关系式;
(2)求经过多少小时,两车之间的距离为120千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题发现
问题发现
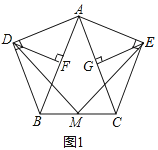
在等腰三角形ABC中,![]() ,分别以AB和AC为斜边,向
,分别以AB和AC为斜边,向![]() 的外侧作等腰直角三角形,如图1所示,其中
的外侧作等腰直角三角形,如图1所示,其中![]() 于点F,
于点F,![]() 于点G,M是BC的中点,连接MD和ME.
于点G,M是BC的中点,连接MD和ME.
填空:线段AF,AG,AB之间的数量关系是______;
线段MD,ME之间的数量关系是______.
![]() 拓展探究
拓展探究
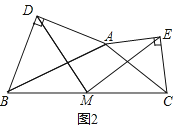
在任意三角形ABC中,分别以AB和AC为斜边向![]() 的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
![]() 解决问题
解决问题
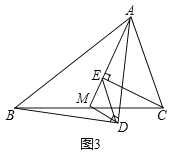
在任意三角形ABC中,分别以AB和AC为斜边,向![]() 的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若
的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若![]() ,请直接写出线段DE的长.
,请直接写出线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,决定开设以下社团活动项目:![]() 文学社
文学社![]() 艺术社
艺术社![]() 体育社
体育社![]() 科创社,为了解学生最喜欢哪一种社团活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图,其中图
科创社,为了解学生最喜欢哪一种社团活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图,其中图![]() 中A所占扇形的圆心角为
中A所占扇形的圆心角为![]() 请回答下列问题:
请回答下列问题:

![]() 这次被调查的学生共有______人;
这次被调查的学生共有______人;
![]() 请你将条形统计图
请你将条形统计图![]() 补充完整;
补充完整;
![]() 在平时的科创社活动中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加科创比赛,求恰好选中甲、乙两位同学的概率
在平时的科创社活动中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加科创比赛,求恰好选中甲、乙两位同学的概率![]() 用树状图或列表法解答
用树状图或列表法解答![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 关于直线
关于直线![]() 对称的图形△
对称的图形△![]() 并写出△
并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向左平移2个单位,作出平移后的△
向左平移2个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请指出对称轴,并求
,它们是否关于某直线对称?若是,请指出对称轴,并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() <
<![]() <
<![]() ,
,
设![]() =3+k(0<k<1).
=3+k(0<k<1).
∴![]() .
.
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈![]() .
.
∴![]() ≈3+
≈3+![]() ≈3.67.
≈3.67.
问题:
(1)请你依照小明的方法,估算![]() 的近似值;
的近似值;
(2)请结合上述具体实例,概括出估算![]() 的公式:已知非负整数a、b、m,若a<
的公式:已知非负整数a、b、m,若a<![]() <a+1,且m=a2+b,则
<a+1,且m=a2+b,则![]() ≈ (用含a、b的代数式表示);
≈ (用含a、b的代数式表示);
(3)请用(2)中的结论估算![]() 的近似值.
的近似值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com