
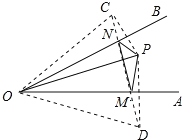
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
【答案】B
【解析】
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=DM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB![]() ∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示.
∵点P关于OA的对称点为D,关于OB的对称点为C,∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB,∴OC=OP=OD,∠AOB![]() ∠COD.
∠COD.
∵△PMN周长的最小值是6cm,∴PM+PN+MN=6,∴DM+CN+MN=6,即CD=6=OP,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°.
故选B.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件,若销售单价每涨1元,每周销售量就减少10件.设销售单价为每件x元(x≥50),一周的销售量为y件.
(1)写出y与x的函数关系式.(标明x的取值范围)
(2)设一周的销售利润为S,写出S与x的函数关系式,并确定当单价在什么范围内变化时,利润随着单价的增大而增大?
(3)在超市对该种商品投入不超过10 000元的情况下,使得一周销售利润达到8 000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护和改善环境,发展新经济,国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展,为响应号召,某市某汽车专卖店销售A,B两种型号的新能源汽车共25辆,这两种型号的新能源汽车的进价、售价如下表:
进价 | 售价 | |
A型 | 10 |
|
B型 | 15 |
|
![]() 如何进货,进货款恰好为325万元?
如何进货,进货款恰好为325万元?
![]() 如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的
如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一个矩形ABCD及![]() 给出如下定义:在同一平面内,如果
给出如下定义:在同一平面内,如果![]() 上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是
上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是![]() 的“随从矩形”
的“随从矩形”![]() 如图,在平面直角坐标系xOy中,直线l:
如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,
交x轴于点M,![]() 的半径为4,矩形ABCD沿直线运动
的半径为4,矩形ABCD沿直线运动![]() 在直线l上
在直线l上![]() ,
,![]() ,
,![]() 轴,当矩形ABCD是
轴,当矩形ABCD是![]() 的“随从矩形”时,点A的坐标为______.
的“随从矩形”时,点A的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
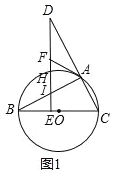
【题目】如图1,BC是![]() 的直径,点A在
的直径,点A在![]() 上,点D在CA的延长线上,
上,点D在CA的延长线上,![]() ,垂足为点E,DE与
,垂足为点E,DE与![]() 相交于点H,与AB相交于点
相交于点H,与AB相交于点![]() 过点A作
过点A作![]() ,与DE相交于点F.
,与DE相交于点F.
![]() 求证:AF为
求证:AF为![]() 的切线;
的切线;
![]() 当
当![]() ,且
,且![]() 时,求:
时,求:![]() 的值;
的值;
![]() 如图2,在
如图2,在![]() 的条件下,延长FA,BC相交于点G,若
的条件下,延长FA,BC相交于点G,若![]() ,求线段EH的长.
,求线段EH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为( )
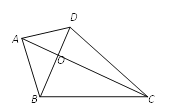
A.48B.42C.36D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com