
【题目】如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为( )
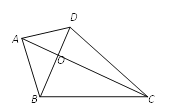
A.48B.42C.36D.32
【答案】B
【解析】
如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.由△POD∽△BOC,得![]() ,设OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由
,设OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由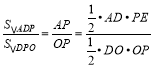 ,推出
,推出![]() ,推出AD=2(4-x),在Rt△ADO中,根据AD2=AO2+DO2,可得4(4-x)2=4x2+42,求出x的值,再根据S四边形ABCD=S△ABD+S△BDC=
,推出AD=2(4-x),在Rt△ADO中,根据AD2=AO2+DO2,可得4(4-x)2=4x2+42,求出x的值,再根据S四边形ABCD=S△ABD+S△BDC=![]() BDAO+
BDAO+![]() BDOC=
BDOC=![]() BD(OA+OC)计算即可.
BD(OA+OC)计算即可.
如图,作∠ADO的平分线DP交AC于P,作PE⊥AD于E.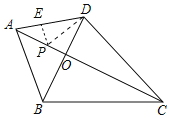
∵∠ADO=2∠BCO,
∴∠PDO=∠BCO,
∵∠POD=∠BOC,
∴△POD∽△BOC,
∴![]() ,设OP=x,
,设OP=x,
∴![]() ,
,
∴OD=2x,
∵PE⊥AD,PO⊥DO,∠PDE=∠PDO,
∴PE=OP,
∴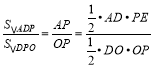 ,
,
∴![]() ,
,
∴AD=2(4-x),
在Rt△ADO中,∵AD2=AO2+DO2,
∴4(4-x)2=4x2+42,
∴x=![]() ,
,
∴OD=3,
∴S四边形ABCD=S△ABD+S△BDC=![]() BDAO+
BDAO+![]() BDOC=
BDOC=![]() BD(OA+OC)=
BD(OA+OC)=![]() ×7×12=42.
×7×12=42.
故选B.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD是一个长方形,将AD沿某一直线AF(F为折痕与CD边的交点)折叠,使点D落在BC边上的某一点E处,请用没有刻度的直尺与圆规找出点E与折痕AF,并在折痕AF上找一点P满足BP+EP最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() <
<![]() <
<![]() ,
,
设![]() =3+k(0<k<1).
=3+k(0<k<1).
∴![]() .
.
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈![]() .
.
∴![]() ≈3+
≈3+![]() ≈3.67.
≈3.67.
问题:
(1)请你依照小明的方法,估算![]() 的近似值;
的近似值;
(2)请结合上述具体实例,概括出估算![]() 的公式:已知非负整数a、b、m,若a<
的公式:已知非负整数a、b、m,若a<![]() <a+1,且m=a2+b,则
<a+1,且m=a2+b,则![]() ≈ (用含a、b的代数式表示);
≈ (用含a、b的代数式表示);
(3)请用(2)中的结论估算![]() 的近似值.
的近似值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
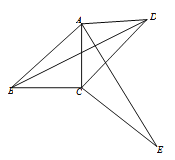
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求四边形ABCD的对角线BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
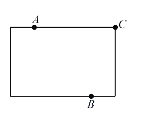
(1)为进一步打造“宜居北京”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉 ![]() 到广场的两个入口
到广场的两个入口 ![]() ,
,![]() 的距离相等,且到广场管理处
的距离相等,且到广场管理处 ![]() 的距离等于
的距离等于 ![]() 和
和 ![]() 之间距离的一半,
之间距离的一半,![]() ,
,![]() ,
,![]() 的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉
的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉 ![]() 的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
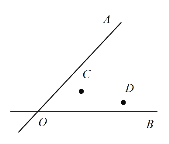
(2)如图,两条公路 ![]() 和
和 ![]() 相交于
相交于 ![]() 点,在
点,在 ![]() 的内部有工厂
的内部有工厂 ![]() 和
和 ![]() ,现要修建一个货站
,现要修建一个货站 ![]() ,使货站
,使货站 ![]() 到两条公路
到两条公路 ![]() ,
,![]() 的距离相等,且到两工厂
的距离相等,且到两工厂 ![]() ,
,![]() 的距离相等,用尺规作出货站
的距离相等,用尺规作出货站 ![]() 的位置.(要求:不写作法,保留作图痕迹,必须用铅笔作图)
的位置.(要求:不写作法,保留作图痕迹,必须用铅笔作图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步降低机动车污染物排放,减轻重污染天气污染发生频次和污染程度,保障人民群众身体健康,郑州市从2017年12月4日0时至2017年12月31日24时起对机动车实施单双号限行措施,此次限行将会大大减少空气中![]() 的排放量,
的排放量,![]() 指的是雾天气时大气中直径小于或等于
指的是雾天气时大气中直径小于或等于![]() 的颗粒物,将
的颗粒物,将![]() 用科学记数法表示为
用科学记数法表示为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com