
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
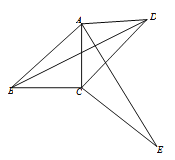
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求四边形ABCD的对角线BD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由旋转的性质可得AC=BC,∠DBC=∠CAE,即可得∠ACB=90°,根据直角三角形的性质可得AE⊥BD,
(2)由旋转的性质可得CD=CE=3,BD=AE,∠DCE=∠ACB=90°,由勾股定理可求BD的长.
(1)如图,设AC与BD的交点为点M,BD与AE的交点为点N,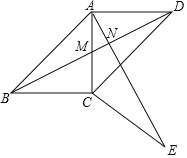
∵旋转
∴AC=BC,∠DBC=∠CAE
又∵∠ABC=45°,
∴∠ABC=∠BAC=45°,
∴∠ACB=90°,
∵∠DBC+∠BMC=90°
∴∠AMN+∠CAE=90°
∴∠AND=90°
∴AE⊥BD,
(2)如图,连接DE,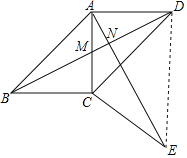
∵旋转
∴CD=CE=3,BD=AE,∠DCE=∠ACB=90°
∴DE=![]() =3
=3![]() ,∠CDE=45°
,∠CDE=45°
∵∠ADC=45°
∴∠ADE=90°
∴EA=![]() =
=![]()
∴BD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与x轴交于点O,
,它与x轴交于点O,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;
;![]() 如此进行下去,得到一“波浪线”,若点
如此进行下去,得到一“波浪线”,若点![]() 在此“波浪线”上,则m的值为
在此“波浪线”上,则m的值为![]()
![]()
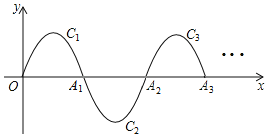
A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.

(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC⊥BD于点O,且AO=BO=4,CO=8,∠ADB=2∠ACB,则四边形ABCD的面积为( )
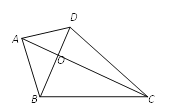
A.48B.42C.36D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一块三角形状的土地平均分给四户人家,现有四种不同的分法,![]() 如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点
如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点![]() ,其中正确的分法有
,其中正确的分法有![]()
![]()

A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com