
【题目】![]() 问题发现
问题发现
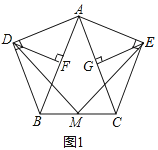
在等腰三角形ABC中,![]() ,分别以AB和AC为斜边,向
,分别以AB和AC为斜边,向![]() 的外侧作等腰直角三角形,如图1所示,其中
的外侧作等腰直角三角形,如图1所示,其中![]() 于点F,
于点F,![]() 于点G,M是BC的中点,连接MD和ME.
于点G,M是BC的中点,连接MD和ME.
填空:线段AF,AG,AB之间的数量关系是______;
线段MD,ME之间的数量关系是______.
![]() 拓展探究
拓展探究
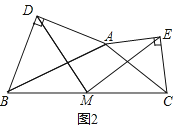
在任意三角形ABC中,分别以AB和AC为斜边向![]() 的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
![]() 解决问题
解决问题
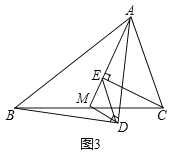
在任意三角形ABC中,分别以AB和AC为斜边,向![]() 的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若
的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若![]() ,请直接写出线段DE的长.
,请直接写出线段DE的长.
【答案】![]()
![]()
【解析】
(1)由条件可以通过三角形全等和轴对称的性质,直角三角形的性质得出结论;
(2)取AB、AC的中点F、G,连接DF,MF,EG,MG,根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形,从而得出△DFM≌△MGE,根据其性质就可以得出结论;
(3)取AB、AC的中点F、G,连接DF,MF,EG,MG,DF和MG相交于H,根据三角形的中位线的性质K可以得出△DFM≌△MGE,由全等三角形的性质和勾股定理就可以得出答案.
![]() ,理由如下:
,理由如下:
![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]()
![]() 在
在![]() 和
和![]() 中,
中,
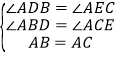 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() 于点F,
于点F,![]() 于点G,
于点G,
![]() ,
,![]() .
.
![]() ,
,
![]() ;
;
![]() ,理由如下:
,理由如下:
![]() 是BC的中点,
是BC的中点,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
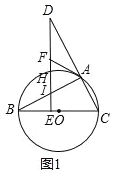
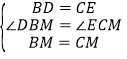 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
故答案为:![]() ;
;![]() ;
;
![]() ,
,![]() .
.
理由如下:
取AB,AC的中点F,G,连接DF,FM,MG,EG,设AB与DM交于点H,如图2,

![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() .
.
![]() 点M是BC的中点,
点M是BC的中点,
![]() 和MG都是
和MG都是![]() 的中位线,
的中位线,
![]() ,
,![]() ,
,
![]() 四边形AFMG是平行四边形,
四边形AFMG是平行四边形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() ;
;
![]() 线段DE的长为
线段DE的长为![]() ,理由如下:
,理由如下:
分别取AB,AC的中点F,G,连接MF,DF,MG,EG,设DF和MG交于点H,如图3,
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() .
.
![]() 点M是BC的中点,
点M是BC的中点,
![]() 和MG都是
和MG都是![]() 的中位线,
的中位线,
![]() ,
,![]() ,
,
![]() 四边形AFMG是平行四边形,
四边形AFMG是平行四边形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() .
.
![]() ,
,![]() .
.
![]() 即
即![]() .
.
又![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
在![]() 中,
中,![]() ,由勾股定理,得
,由勾股定理,得![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,CD平分∠ACB交AB于点D,AE∥DC交BC的延长线于点E,已知∠BAC=32°,求∠E的度数为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护和改善环境,发展新经济,国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展,为响应号召,某市某汽车专卖店销售A,B两种型号的新能源汽车共25辆,这两种型号的新能源汽车的进价、售价如下表:
进价 | 售价 | |
A型 | 10 |
|
B型 | 15 |
|
![]() 如何进货,进货款恰好为325万元?
如何进货,进货款恰好为325万元?
![]() 如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的
如何进货,该专卖店售完A,B两种型号的新能源汽车后获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )

A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一个矩形ABCD及![]() 给出如下定义:在同一平面内,如果
给出如下定义:在同一平面内,如果![]() 上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是
上存在一点,使得这点到矩形ABCD的四个顶点的距离相等,那么称矩形ABCD是![]() 的“随从矩形”
的“随从矩形”![]() 如图,在平面直角坐标系xOy中,直线l:
如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,
交x轴于点M,![]() 的半径为4,矩形ABCD沿直线运动
的半径为4,矩形ABCD沿直线运动![]() 在直线l上
在直线l上![]() ,
,![]() ,
,![]() 轴,当矩形ABCD是
轴,当矩形ABCD是![]() 的“随从矩形”时,点A的坐标为______.
的“随从矩形”时,点A的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
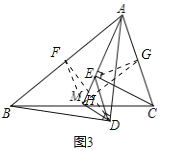
【题目】如图1,BC是![]() 的直径,点A在
的直径,点A在![]() 上,点D在CA的延长线上,
上,点D在CA的延长线上,![]() ,垂足为点E,DE与
,垂足为点E,DE与![]() 相交于点H,与AB相交于点
相交于点H,与AB相交于点![]() 过点A作
过点A作![]() ,与DE相交于点F.
,与DE相交于点F.
![]() 求证:AF为
求证:AF为![]() 的切线;
的切线;
![]() 当
当![]() ,且
,且![]() 时,求:
时,求:![]() 的值;
的值;
![]() 如图2,在
如图2,在![]() 的条件下,延长FA,BC相交于点G,若
的条件下,延长FA,BC相交于点G,若![]() ,求线段EH的长.
,求线段EH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com