Question

6．在矩形ABCD中，AB=2，AD=5，将一直角尺的顶点放在AD上的点P处（AP＜PD），直角尺的两直角边分别交矩形边于点E，F，连接EF（图1）．当点E在点B时，点F恰好与点C重合（图2）．
（1）求（图2）中AP的长；
（2）将直角尺绕（1）中的点P逆时针旋转，点E从点A的位置开始．
①如果旋转到图（2）的位置停止，在这个过程中，tan∠PEF的值是否发生变化？若不变，请求出这个值，若变化，请说明理由；
②如果旋转到点F在点D的位置，直接写出线段EF的中点经过的路线长．

Answer 1

分析 （1）如答图1，利用互余关系证明△APB∽△DCP，利用相似比求AP；
（2）①tan∠PEF的值不变．如答图2，过F作FG⊥AD，垂足为G，同（1）的方法证明△APB∽△DCP，得相似比$\frac{PF}{PE}$=$\frac{GF}{AP}$=$\frac{2}{1}$=2，再利用锐角三角函数的定义求值；
②如答图4，画出起始位置和终点位置时，线段EF的中点Q₁，Q₂，连接Q₁Q₂，线段Q₁Q₂即为线段EF的中点经过的路线长，也就是△BPC的中位线．

解答 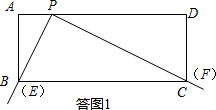解：（1）如答图1，在矩形ABCD中，∠A=∠D=90°，
∴∠ABP+∠APB=90°，
又∵∠BPC=90°，
∴∠APB+∠DPC=90°，
∴∠ABP=∠DPC，
∴△APB∽△DCP，
∴$\frac{AP}{CD}$=$\frac{AB}{DP}$，即$\frac{AP}{2}$=$\frac{2}{5-AP}$，
∴AP=1，AP=4（舍去）；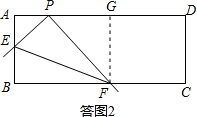

（2）①
①∠PEF的大小不变．
理由：过点F作FG⊥AD于点G，如答图2．
∵∠A=∠B=∠AGF=90°，
∴∠AEP+∠APE=90°，四边形ABFG是矩形．
∴GF=AB=2．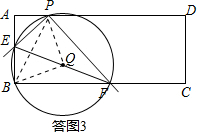
∵∠EPF=90°，
∴∠APE+∠GPF=90°．
∴∠GPF=∠AEP．
∴△GPF∽△AEP．
∴$\frac{PF}{PE}$=$\frac{GF}{AP}$=$\frac{2}{1}$=2．
在Rt△EPF中，
∵tan∠PEF=2；

②取EF的中点Q，连接BQ，PQ，PB，如答图3．
∵∠EBF=∠EPF=90°，点Q为EF的中点，
∴QP=$\frac{1}{2}$EF=QB，
∴点Q在线段PB的垂直平分线上．
如答图4，当点E在点B处时，点Q在BC中点Q₁处；
当点E在点A处时，点Q在PB的中点Q₂处．根据三角形中位线定理得Q₁Q₂=$\frac{1}{2}$PC=$\sqrt{5}$．
∴Q₂Q₃=$\frac{1}{2}\sqrt{5}$．
所以从开始到停止，线段EF的中点Q所经过的路线长Q₁Q₃为$\frac{3}{2}\sqrt{5}$．

点评 本题考查了四边形综合题，解题时需要掌握相似三角形的判定与性质，矩形的性质，解直角三角形．解答该题的关键是利用互余关系证明相似三角形：△APB∽△DCP．