
如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC= .
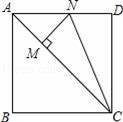

67.5° .
【考点】全等三角形的判定与性质;角平分线的性质;正方形的性质.
【分析】根据HL先证明两个直角△NMC和直角△NDC全等,得出∠DCN=∠MCN,再根据三角形的内角和定理即可求出∠MNC的度数.
【解答】解:∵正方形ABCD中,
∴∠DCA=45°,∠NDC=90°,
∵MN⊥AC,
∴∠NMC=90°,
在Rt△NMC和Rt△NDC中,

 ,
,
∴Rt△NMC≌Rt△NDC(HL),
∴∠DCN=∠MCN,
∴∠DCN=∠MCN=22.5°,
∴∠MNC=67.5°;
故答案为:67.5°.
【点评】本题主要考查了正方形的性质及直角三角形的全等判定,结合已知和图形,准确找到全等三角形全等需要的条件是解答本题的关键.


科目:初中数学 来源: 题型:
在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a﹣b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.不是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在▱ABCD中,下列结论一定正确的是( )
①∠1+∠2=180°
②∠2+∠3=180°
③∠3+∠4=180°
④∠2+∠4=180°.
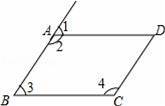

A.①②③ B.②③④ C.①②④ D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com