
【题目】如图点O是等边![]() 内一点,
内一点,![]() ,∠ACD=∠BCO,OC=CD,
,∠ACD=∠BCO,OC=CD,
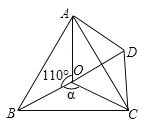
(1)试说明:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)当![]() 为多少度时,
为多少度时,![]() 是等腰三角形
是等腰三角形
【答案】(1)见解析;(2)△AOD是直角三角形,理由见解析;(3) 110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;
(2)先求得∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠CDO=60°,于是可计算出∠ADO=90°,由此可判断△AOD是直角三角形;
(3)先利用α表示出∠ADO=α-60°,∠AOD=190°-α,再进行分类讨论:当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°;当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°;当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,然后分别解方程求出对应的α的值即可.
(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α60°,∠AOD=360°60°110°α=190°α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°α=α60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°α)+α60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°α+2(α60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.例如,一元二次方程的两个根是2和4,则方程x2﹣6x+8=0就是“倍根方程”.
(1)若一元二次方程x2﹣3x+c=0是“倍根方程”,求c的值;
(2)若(x﹣2)(mx﹣n)=0(m≠0)是“倍根方程”,求代数式4m2﹣5mn+n2的值;
(3)若点(p,q)在反比例函数y=![]() 的图象上,请说明关于x的方程px2+3x+q=0是“倍根方程”;
的图象上,请说明关于x的方程px2+3x+q=0是“倍根方程”;
(4)若关于x的一元二次方程ax2+bx+c=0(a≠0)是“倍根方程”,请说明2b2=9ac.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
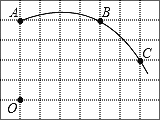
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,只借助直尺确定该圆弧所在圆的圆心D,并连接AD、CD.(保留作图痕迹,不写作法)
(2)请在(1)的基础上,完成下列填空与计算:
①写出点的坐标:C 、D ;
②⊙D的半径= ;(结果保留根号)
③求扇形ADC的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,FE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为![]() ,其中正确的是( )
,其中正确的是( )
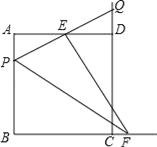
A. ①② B. ①②④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
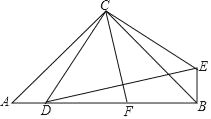
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为2的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作s1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作s2.照此规律作下去,则s2019=_____.
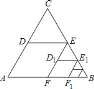
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com