
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径
的路径![]() 运动一周,且速度为每秒
运动一周,且速度为每秒![]() ,设运动的时间为
,设运动的时间为![]() 秒.
秒.
(![]() )求
)求![]() 为何值时,
为何值时,![]() 把
把![]() 的周长分成相等的两部分
的周长分成相等的两部分
(![]() )求
)求![]() 为何值时,
为何值时,![]() 把
把![]() 的面积分成相等的两部分;并求此时
的面积分成相等的两部分;并求此时![]() 的长.
的长.
(![]() )求
)求![]() 为何值时,
为何值时,![]() 为等腰三角形?(请直接写出答案)
为等腰三角形?(请直接写出答案)


【答案】(![]() )
)![]() ;(
;(![]() )5cm;(
)5cm;(![]() )
)![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.
【解析】试题分析:(1)先由勾股定理求出△ABC的斜边AB=10cm,则△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,即可得2t=12,解方程即可求t值;(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;(3)△BCP为等腰三角形时,分三种情况①CP=CB;②BC=BP;③PB=PC,根据这三种情况分别求得t值即可.
试题解析:
(![]() )∵
)∵![]() ,
,![]() ,
,
∴![]() ,
,
依题意得![]() ,
,
得![]() ,
,
∴![]() 时,
时,![]() 把
把![]() 周长分成相等两部分.
周长分成相等两部分.
(![]() )
)![]() 要把
要把![]() 面积分成两部分且相等,
面积分成两部分且相等,
∴![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
得![]() ,
,
此时![]() .
.
(![]() )
)![]() 为等腰三角形,共有三种情况,
为等腰三角形,共有三种情况,
①![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
![]() ,
,![]() 在
在![]() 上,此时可求得
上,此时可求得![]() ,∴
,∴![]() ,
,
∴![]() .
.
②![]() ,点
,点![]() 在
在![]() 上,
上,
![]() ,
,![]() ,
,
∴![]() .
.
③![]() ,点
,点![]() 在
在![]() 的垂直平分线上与
的垂直平分线上与![]() 的交点处,即为
的交点处,即为![]() 中点,
中点,
有![]() ,
,
综上可知,![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
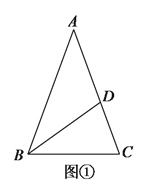
【题目】(![]() )如图①,在
)如图①,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数.
的度数.
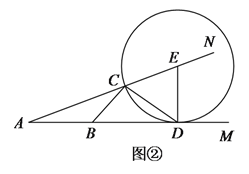
(![]() )如图②,点
)如图②,点![]() ,
,![]() 在射线
在射线![]() 上,点
上,点![]() ,
,![]() 在射线
在射线![]() 上,且
上,且![]() .
.
①若![]() ,求
,求![]() 的度数.
的度数.
②若以![]() 为圆心,
为圆心,![]() 为半径作弧,与射线
为半径作弧,与射线![]() 上没有交点(除
上没有交点(除![]() 点外),直接写出
点外),直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在8×8的网络中,△ABC是格点三角形(顶点是网格线的交点),若点A坐标为(-1,3),按要求回答下列问题:
(1)建立符合条件的平面直角坐标系,并写出点B和点C的坐标;
(2)将△ABC先向下平移2个单位长度,在向右平移3个单位长度,得到△DEF,请在图中画出△DEF,并求出线段AC在平移过程中扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 相等的角是对顶角
B. 若直线a与b互相垂直,记作a∥b
C. 内错角相等
D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,因式分解正确的是( )
A. 2a2﹣2=2(a+1)(a﹣1) B. (a+3)(a﹣3)=a2﹣9
C. ﹣ab2+2ab﹣3b=﹣b(ab﹣2a﹣3) D. x2﹣2x﹣3=x(x﹣2)﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com