
【题目】已知△ABC是等边三角形,点P在射线AC上(点P与点A、点C不重合),点D在线段BC的延长线上,且AP=CD,△PCD′与△PCD关于直线AC对称.
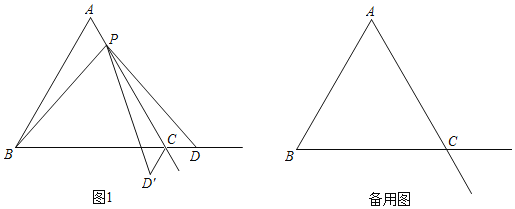
(1)如图1,当点P在线段AC上时,
①求证:PB=PD;
②请求出∠BPD′的度数;
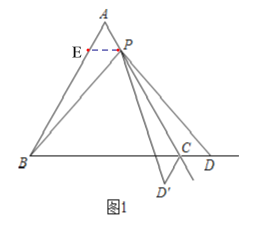
(2)当点P在射线AC上运动时,请直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
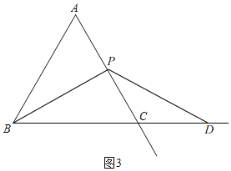
(3)将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能否重合?若能重合,请直接写出旋转的角度;若不能重合,请说明理由;
(4)若AB=4,当点P为AC边的中点时,请直接写出PD'的长
【答案】(1)①见解析;②60°;(2)①成立,理由见解析;②∠BPD′的度数不发生变化,理由见解析;(3)PD′与PB能重合,旋转的角度为60°;(4)PD'=2![]()
【解析】
(1)①过点P作PE∥BC交AB于E,易证△APE是等边三角形,得AP=PE,BE=PC,∠BEP=∠PCD,从而得:△BPE≌△PDC,即可得到结论;②由△BPE≌△PDC,得∠PBE=∠DPC,进而得∠PBE=∠D'PC,由∠BPC=∠A+∠PBE=60°+∠D'PC,即可得到结论;
(2)①过点P作PE∥BC交AB的延长线于E,易证△APE是等边三角形,得AP=PE,BE=PC,∠BEP=∠PCD=60°,得△BPE≌△PDC(SAS),即可得到结论;②由△BPE≌△PDC,得∠PBE=∠DPC,进而得∠PBE=∠D'PC,即可得到结论.
(3)由(1)(2)知,∠BPD'=60°,PB=PD=PD',即可得到结论;
(4)由△ABC是等边三角形,点P是AC的中点,得AP=2,BP⊥AC,根据勾股定理得BP的值,进而即可得到答案.
(1)①∵△ABC是等边三角形,
∴AB=AC,∠A=∠ABC=∠ACB=60°,
过点P作PE∥BC交AB于E,如图1,
∴∠AEP=∠ABC=60°,∠APE=∠ACB=60°,
∴∠AEP=∠APE=∠A=60°,
∴△APE是等边三角形,
∴AP=PE,
∴AB﹣AE=AC﹣AP,
∴BE=PC,
∵AP=CD,
∴PE=CD,
∵∠BEP=180°﹣∠AEP=120°,∠PCD=180°﹣∠ACB=120°,
∴∠BEP=∠PCD,
∴△BPE≌△PDC(SAS),
∴PB=PD;
②由①知,△BPE≌△PDC,
∴∠PBE=∠DPC,
∵△PCD′与△PCD关于直线AC对称,
∴∠DPC=∠D'PC,
∴∠PBE=∠D'PC,
∵∠BPC=∠A+∠PBE=60°+∠D'PC,
∴∠BPD'=∠BPC﹣∠D'PC=60°;
(2)①PB=PD仍然成立,理由如下:
∵△ABC是等边三角形,
∴AB=AC,∠A=∠ABC=∠ACB=60°,
∴∠DCP=60°
过点P作PE∥BC交AB的延长线于E,如图2,
∴∠AEP=∠ABC=60°,∠APE=∠ACB=60°,
∴∠AEP=∠APE=∠A=60°,
∴△APE是等边三角形,
∴AP=PE,
∴AE﹣AB=AP﹣AC,
∴BE=PC,
∵AP=CD,
∴PE=CD,
∵∠BEP=∠PCD=60°
∴△BPE≌△PDC(SAS),
∴PB=PD;
②∠BPD′的度数不发生变化,理由如下:
由①知,△BPE≌△PDC,
∴∠PBE=∠DPC,
∵△PCD′与△PCD关于直线AC对称,
∴∠DPC=∠D'PC,
∴∠PBE=∠D'PC,
∴∠BPD'=∠D'PC﹣∠BPC=∠PBE﹣∠BPC
=∠PBE﹣(∠APE﹣∠BPE)
=∠PBE﹣(60°﹣∠BPE)
=∠PBE+∠BPE﹣60°
=180°﹣∠AEP﹣60°
=180°﹣60°﹣60°
=60°;
(3)∵由(1)(2)知,∠BPD'=60°,PB=PD=PD',
∴将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能重合,
∴旋转的角度为60°;
(4)如图3,由(1)知,BP=PD,由对称得,PD=PD',
∴BP=PD',
∵△ABC是等边三角形,点P是AC的中点,
∴AP=![]() AC=
AC=![]() AB=2,BP⊥AC,
AB=2,BP⊥AC,
∴∠APB=90°,
在Rt△ABP中,根据勾股定理得,BP=![]() ,
,
∴PD'=2![]() .
.



科目:初中数学 来源: 题型:
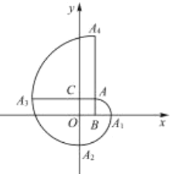
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧.继续以点
为半径的圆弧.继续以点![]() ,
,![]() ,
,![]() ,
,![]() 为圆心按上述作法得到的曲线
为圆心按上述作法得到的曲线![]() …称为正方形的“渐开线”,则点
…称为正方形的“渐开线”,则点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
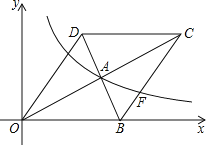
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
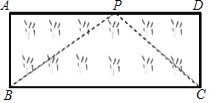
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )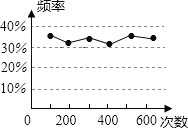
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
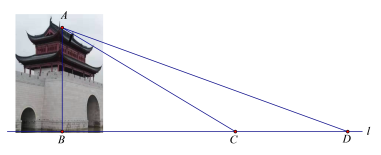
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
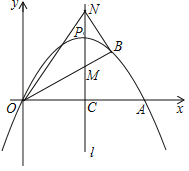
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
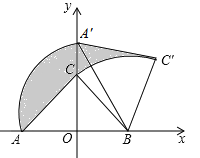
【题目】如图,![]() 中,
中,![]() ,
,![]() ,在以
,在以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立的平面直角坐标系中,将
轴建立的平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 旋转至
旋转至![]() 轴的正半轴上的点
轴的正半轴上的点![]() 处,若
处,若![]() ,则图中阴影部分面积为________.
,则图中阴影部分面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
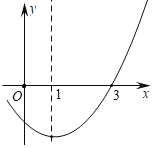
【题目】若二次函数y=x2﹣2x+k的部分图象如图所示,则关于x的一元二次方程x2﹣2x+k=0的解一个为x1=3,则方程x2﹣2x+k=0另一个解x2=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com