
【题目】如图,![]() 中,
中,![]() ,
,![]() ,在以
,在以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立的平面直角坐标系中,将
轴建立的平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 旋转至
旋转至![]() 轴的正半轴上的点
轴的正半轴上的点![]() 处,若
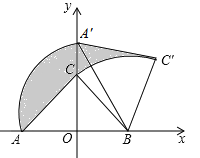
处,若![]() ,则图中阴影部分面积为________.
,则图中阴影部分面积为________.
【答案】![]()
【解析】
根据等腰直角三角形的性质求出AB,再根据旋转的性质可得A′B=AB,然后求出∠OA′B=30°,再根据直角三角形两锐角互余求出∠A′BA=60°,即旋转角为60°,再根据S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′=S扇形ABA′-S扇形CBC′,然后利用扇形的面积公式列式计算即可得解.
解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=4,BC=2![]() ,
,
∵△ABC绕点B顺时针旋转点A在A′处,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋转角为60°,
S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′,
=S扇形ABA′-S扇形CBC′,
= ![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
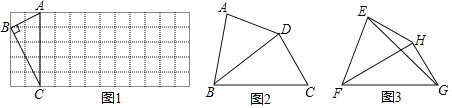
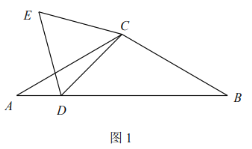
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
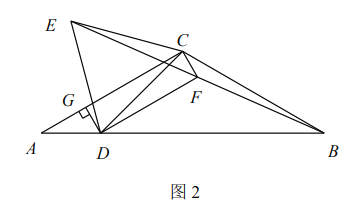
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
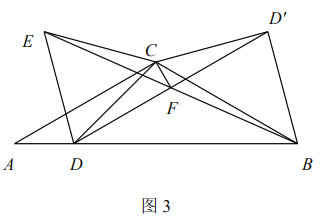
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点P在射线AC上(点P与点A、点C不重合),点D在线段BC的延长线上,且AP=CD,△PCD′与△PCD关于直线AC对称.
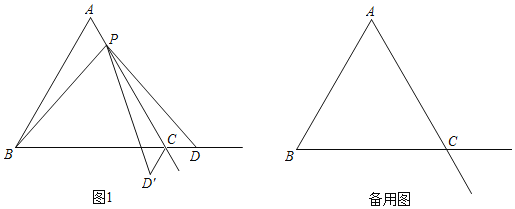
(1)如图1,当点P在线段AC上时,
①求证:PB=PD;
②请求出∠BPD′的度数;
(2)当点P在射线AC上运动时,请直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
(3)将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能否重合?若能重合,请直接写出旋转的角度;若不能重合,请说明理由;
(4)若AB=4,当点P为AC边的中点时,请直接写出PD'的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯下,广告标杆AB的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵树,它的影子是MN.
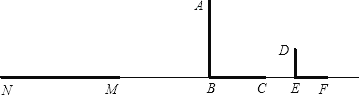
(1)请在图中画出表示树高的线段.(不写作法,保留作图痕迹)
(2)若已知点N、F到路灯的底部距离相等,小明身高1.6米,影长EF为1.8米,树的影长MN是6米,请计算树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠ADC=90°,AD∥BC,点E在BC上,点F在AC上,∠DFC=∠AEB.
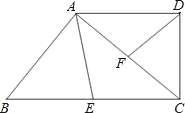
(1)求证:△ADF∽△CAE;
(2)当AD=8,DC=6,点E、F分别是BC、AC的中点时,求BC的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
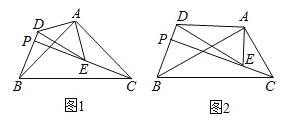
(1)问题提出:如图1,若![]() ,
,![]() .
.
①![]() 与
与![]() 的数量关系为________;
的数量关系为________;
②![]() 的度数为________.
的度数为________.
(2)猜想论证:如图2,若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
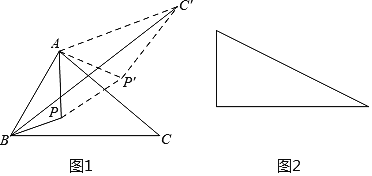
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() .
.
![]() 如图1,若
如图1,若![]() 求等边
求等边![]() 的边长;
的边长;
![]() 如图2,点
如图2,点![]() 在
在![]() 边上移动过程中,连接
边上移动过程中,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
①求证:![]() ;
;
②如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com