
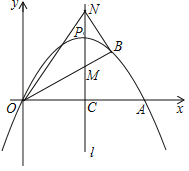
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.
【答案】(1)二次函数的关系式为![]() ;(2)①
;(2)①![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() ;②见解析
;②见解析
【解析】
(1)利用待定系数法即可得到答案;
(2)①设![]() ,由点的对称性得到
,由点的对称性得到![]() ,再由勾股定理得到答案;②设直线
,再由勾股定理得到答案;②设直线![]() 与x轴交于点D,求得直线
与x轴交于点D,求得直线![]() 解析式,再结合题意即可得到答案.
解析式,再结合题意即可得到答案.
解:(1)∵二次函数顶点为![]()
∴设顶点式![]()
∵二次函数图象过点![]()
∴![]() ,解得:
,解得:![]()
∴二次函数的关系式为![]()
(2)设![]()
∴直线![]() 解析式为:
解析式为:![]()
∵![]() 交对称轴l于点M
交对称轴l于点M
∴当![]() 时,
时,![]()
∴![]()
∵点M、N关于点P对称
∴![]() ,
,
∴![]() ,即
,即![]()
①∵![]()
∴![]()
∴![]()
解得:![]()
∴![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,B
,B![]()
∴![]() ,
,![]()
∴![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() .
.
②证明:如图,设直线![]() 与x轴交于点D
与x轴交于点D
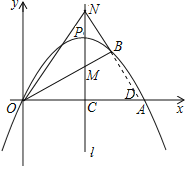
∵![]() 、
、![]()
设直线![]() 解析式为
解析式为![]()
∴ 解得:
解得: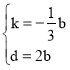
∴直线![]() :
:![]()
当![]() 时,
时,![]() ,解得:
,解得:![]()
∴![]()
∵![]() ,
,![]() 轴
轴
∴![]() 垂直平分
垂直平分![]()
∴![]()
∴![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式,现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆渴乐自驾游公司在元旦节推出四条自驾线路,为调查客户对各条线路的喜欢情况,微信群里做了一次“我最期待的自驾线路”问卷调查(群里每个人都进行了调查且只选择一条线路),统计后发现选湘西的人数比选毕棚沟的少6人;选邛海的人数不仅比选毕棚沟的多,且为整数倍:选毕棚沟与邛海的人数之和是选择湘西和北海的人数之和的4倍;选北海和邛海的人数之和比选湘西与毕棚沟的人数之和多22人,则该微信群里参与调查的共_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点P在射线AC上(点P与点A、点C不重合),点D在线段BC的延长线上,且AP=CD,△PCD′与△PCD关于直线AC对称.
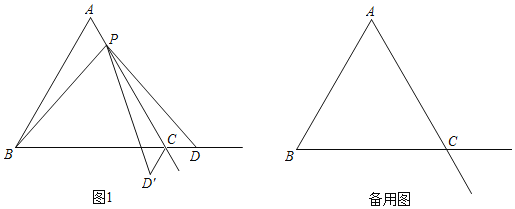
(1)如图1,当点P在线段AC上时,
①求证:PB=PD;
②请求出∠BPD′的度数;
(2)当点P在射线AC上运动时,请直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
(3)将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能否重合?若能重合,请直接写出旋转的角度;若不能重合,请说明理由;
(4)若AB=4,当点P为AC边的中点时,请直接写出PD'的长
查看答案和解析>>
科目:初中数学 来源: 题型:
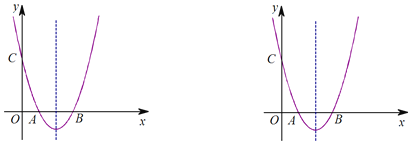
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求该抛物线的表达式及顶点坐标;
(2)点![]() 为抛物线上一点(不与点
为抛物线上一点(不与点![]() 重合),联结
重合),联结![]() .当
.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点
轴的方向向下平移,平移后的抛物线的顶点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,当
,当![]() 时,求抛物线平移的距离.
时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯下,广告标杆AB的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵树,它的影子是MN.
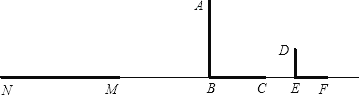
(1)请在图中画出表示树高的线段.(不写作法,保留作图痕迹)
(2)若已知点N、F到路灯的底部距离相等,小明身高1.6米,影长EF为1.8米,树的影长MN是6米,请计算树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠ADC=90°,AD∥BC,点E在BC上,点F在AC上,∠DFC=∠AEB.
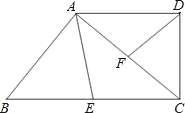
(1)求证:△ADF∽△CAE;
(2)当AD=8,DC=6,点E、F分别是BC、AC的中点时,求BC的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
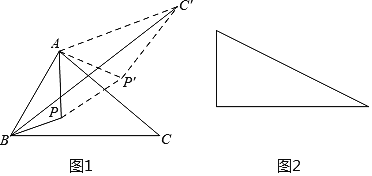
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
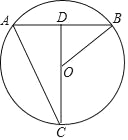
【题目】如图,点C在⊙O上,联结CO并延长交弦AB于点D, ![]() ,联结AC、OB,若CD=40,AC=20
,联结AC、OB,若CD=40,AC=20![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com