
ЁОЬтФПЁПдкГѕжаНзЖЮЕФКЏЪ§бЇЯАжаЃЌЮвУЧОРњСЫСаБэЁЂУшЕуЁЂСЌЯпЛКЏЪ§ЭМЯѓЃЌВЂНсКЯЭМЯѓбаОПКЏЪ§аджЪЕФЙ§ГЬЃЎвдЯТЪЧЮвУЧбаОПКЏЪ§![]() аджЪМАЦфгІгУЕФВПЗжЙ§ГЬЃЌЧыАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
аджЪМАЦфгІгУЕФВПЗжЙ§ГЬЃЌЧыАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
ЃЈ1ЃЉЧыАбЯТБэВЙГфЭъећЃЌВЂдкЭМжаВЙШЋИУКЏЪ§ЭМЯѓЃЛ
| Ё | Ѓ5 | Ѓ4 | Ѓ3 | Ѓ2 | Ѓ1 | 0 | 1 | 2 | 3 | 4 | 5 | Ё |
| Ё |
|
|
| Ѓ3 | 0 | 3 |
|
|
| Ё |
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЃЌХаЖЯЯТСаЙигкИУКЏЪ§аджЪЕФЫЕЗЈЪЧЗёе§ШЗЃЌе§ШЗЕФдкЯргІЕФРЈКХФкДђЁАЁЬЁБЃЌДэЮѓЕФдкЯргІЕФРЈКХФкДђЁАЁСЁБЃЛ
ЂйИУКЏЪ§ЭМЯѓЪЧжсЖдГЦЭМаЮЃЌЫќЕФЖдГЦжсЮЊyжсЃЛ( )
ЂкИУКЏЪ§дкздБфСПЕФШЁжЕЗЖЮЇФкЃЌгазюДѓжЕКЭзюаЁжЕЃЌЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ
ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ( )
ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ( )
ЂлЕБ![]() Лђ
Лђ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ( )
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ( )
ЃЈ3ЃЉвбжЊКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌНсКЯФуЫљЛЕФКЏЪ§ЭМЯѓЃЌжБНгаДГіВЛЕШЪН
ЕФЭМЯѓШчЭМЫљЪОЃЌНсКЯФуЫљЛЕФКЏЪ§ЭМЯѓЃЌжБНгаДГіВЛЕШЪН![]() ЕФНтМЏЃЈБЃСє1ЮЛаЁЪ§ЃЌЮѓВюВЛГЌЙ§0.2ЃЉЃЎ
ЕФНтМЏЃЈБЃСє1ЮЛаЁЪ§ЃЌЮѓВюВЛГЌЙ§0.2ЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЂйЁС ЂкЁЬ ЂлЁЬЃЛЃЈ3ЃЉxЃМ1Лђ0.3ЃМxЃМ1.8ЃЎ
ЃЛЃЈ2ЃЉЂйЁС ЂкЁЬ ЂлЁЬЃЛЃЈ3ЃЉxЃМ1Лђ0.3ЃМxЃМ1.8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉДњШыx=3КЭx=-3МДПЩЧѓГіЖдгІЕФyжЕЃЌдйВЙШЋКЏЪ§ЭМЯѓМДПЩЃЛ
ЃЈ2ЃЉНсКЯКЏЪ§ЭМЯѓПЩДгдіМѕадМАЖдГЦадНјааХаЖЯЃЛ
ЃЈ3ЃЉИљОнЭМЯѓЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЕБx=-3ЪБЃЌ![]()
![]() ЃЌ
ЃЌ
ЕБx=3ЪБЃЌ![]()
![]() ЃЌ
ЃЌ
КЏЪ§ЭМЯѓШчЯТЃК
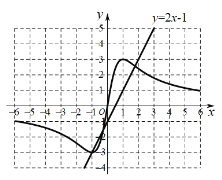
ЃЈ2ЃЉЂйгЩКЏЪ§ЭМЯѓПЩЕУЫќЪЧжааФЖдГЦЭМаЮЃЌВЛЪЧжсЖдГЦЭМаЮЃЛ
ЙЪД№АИЮЊЃКЁС ЃЌ
ЂкНсКЯКЏЪ§ЭМЯѓПЩЕУЃКИУКЏЪ§дкздБфСПЕФШЁжЕЗЖЮЇФкЃЌгазюДѓжЕКЭзюаЁжЕЃЌЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ
ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ
ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ
ЙЪД№АИЮЊЃКЁЬ ЃЌ
ЂлЙлВьКЏЪ§ЭМЯѓПЩЕУЃКЕБ![]() Лђ
Лђ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ
ЙЪД№АИЮЊЃКЁЬЃЎ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]()
![]() ЪБЃЌ
ЪБЃЌ![]()
ЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪИУВЛЕШЪНЕФНтМЏЮЊЃК xЃМ1Лђ0.3ЃМxЃМ1.8ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЩЯЕФвЛЕуЃЌСЌНг
ЩЯЕФвЛЕуЃЌСЌНг![]() ,НЋЁї
,НЋЁї![]() НјааЗелЃЌЧЁКУЪЙЕу
НјааЗелЃЌЧЁКУЪЙЕу![]() Тфдк
Тфдк![]() ЕФжаЕу
ЕФжаЕу![]() ДІЃЌдк
ДІЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЕФГЄЮЊАыОЖзїАыдВгы
ЕФГЄЮЊАыОЖзїАыдВгы![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ;Шє
;Шє![]() ,дђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ ____ ЃЎ
,дђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ ____ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЕиИпЫйЬњТЗНЈЩшГЩЙІЃЌвЛСаЖЏГЕДгМзЕиПЊЭљввЕиЃЌвЛСаЦеЭЈСаГЕДгввЕиПЊЭљМзЕиЃЌСНГЕОљдШЫйааЪЛВЂЭЌЪБГіЗЂЃЌЩшЦеЭЈСаГЕааЪЛЕФЪБМфЮЊxЃЈаЁЪБЃЉЃЌСНГЕжЎМфЕФОрРыЮЊyЃЈЧЇУзЃЉЃЌЭМжаЕФелЯпБэЪОyгыxжЎМфЕФКЏЪ§ЙиЯЕЃЌЯТСаЫЕЗЈЃК
ЂйМзЁЂввСНЕиЯрОр1800ЧЇУзЃЛ
ЂкЕуBЕФЪЕМЪвтвхЪЧСНГЕГіЗЂКѓ4аЁЪБЯргіЃЛ
ЂлmЃН6ЃЌnЃН900ЃЛ
ЂмЖЏГЕЕФЫйЖШЪЧ450ЧЇУз/аЁЪБЃЎ
ЦфжаВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
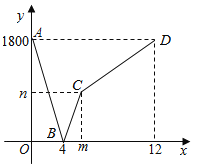
A.ЂйB.ЂкC.ЂлD.Ђм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
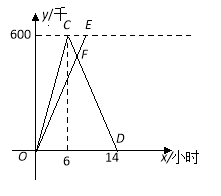
ЁОЬтФПЁПAЃЌBСНГЧЯрОр600ЧЇУзЃЌМзЁЂввСНГЕЭЌЪБДгAГЧГіЗЂЪЛЯђBГЧЃЌМзГЕЕНДяBГЧКѓСЂМДЗЕЛиЃЎШчЭМЪЧЫќУЧРыAГЧЕФОрРыyЃЈЧЇУзЃЉгыааЪЛЪБМф xЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЎ
ЃЈ1ЃЉЧѓМзГЕааЪЛЙ§ГЬжаyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБЫќУЧааЪЛСЫ7аЁЪБЪБЃЌСНГЕЯргіЃЌЧѓввГЕЕФЫйЖШМАввГЕааЪЛЙ§ГЬжаyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБСНГЕЯрОр100ЧЇУзЪБЃЌЧѓМзГЕааЪЛЕФЪБМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОрФГОгУёТЅABТЅЕзBЕузѓВрЫЎЦНОрРы60mЕФCЕуДІгавЛИіЩНЦТЃЌЩНЦТCDЕФЦТЖШЃЈЛђЦТБШЃЉ![]() ЃЌЩНЦТЦТЕзCЕуЕНЦТЖЅDЕуЕФОрРы
ЃЌЩНЦТЦТЕзCЕуЕНЦТЖЅDЕуЕФОрРы![]() ЃЌдкЦТЖЅDЕуДІВтЕУОгУёТЅТЅЖЅAЕуЕФбіНЧЮЊ28ЁуЃЌОгУёТЅABгыЩНЦТCDЕФЦЪУцдкЭЌвЛЦНУцФкЃЌдђОгУёТЅABЕФИпЖШдМЮЊЃЈ ЃЉ
ЃЌдкЦТЖЅDЕуДІВтЕУОгУёТЅТЅЖЅAЕуЕФбіНЧЮЊ28ЁуЃЌОгУёТЅABгыЩНЦТCDЕФЦЪУцдкЭЌвЛЦНУцФкЃЌдђОгУёТЅABЕФИпЖШдМЮЊЃЈ ЃЉ
ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ

A.76.9mB.82.1mC.94.8mD.112.6m
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуAдк
ЃЌЕуAдк![]() ЩЯЃЌЫФБпаЮ
ЩЯЃЌЫФБпаЮ![]() ЪЧОиаЮЃЌСЌНг
ЪЧОиаЮЃЌСЌНг![]() ЁЂ
ЁЂ![]() НЛгкЕуEЃЌСЌНг
НЛгкЕуEЃЌСЌНг![]() НЛ
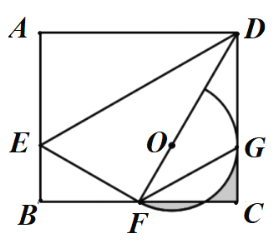
НЛ![]() гкЕуFЃЎЯТСа4ИіХаЖЯЃКЂй
гкЕуFЃЎЯТСа4ИіХаЖЯЃКЂй![]() ЦНЗж
ЦНЗж![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмШєЕуGЪЧЯпЖЮ
ЃЛЂмШєЕуGЪЧЯпЖЮ![]() ЕФжаЕуЃЌдђ
ЕФжаЕуЃЌдђ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЎе§ШЗХаЖЯЕФИіЪ§ЪЧЃЈ ЃЉ
ЮЊЕШбќжБНЧШ§НЧаЮЃЎе§ШЗХаЖЯЕФИіЪ§ЪЧЃЈ ЃЉ

A.4B.3C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊжБЯп
жаЃЌвбжЊжБЯп![]() гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЙ§AЁЂBСНЕуЕФХзЮяЯп
гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЙ§AЁЂBСНЕуЕФХзЮяЯп![]() гыxжсНЛгкСэвЛЕу
гыxжсНЛгкСэвЛЕу![]() ЃЎ
ЃЎ
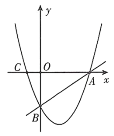
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙ![]() ЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуMЮЊжБЯп![]() ЯТЗНХзЮяЯпЩЯвЛЕуЃЌЕуNЮЊyжсЩЯвЛЕуЃЌЕБ
ЯТЗНХзЮяЯпЩЯвЛЕуЃЌЕуNЮЊyжсЩЯвЛЕуЃЌЕБ![]() ЕФУцЛ§зюДѓЪБЃЌЧѓ
ЕФУцЛ§зюДѓЪБЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГНЬЪвРяШеЙтЕЦЕФЫФИіПижЦПЊЙиЃЈЗжБ№МЧЮЊAЁЂBЁЂCЁЂDЃЉЃЌУПИіПЊЙиЗжБ№ПижЦвЛХХШеЙтЕЦЃЈПЊЙиађКХгыШеЙтЕЦЕФХХЪ§ађКХВЛвЛЖЈвЛжТЃЉЃЎФГЬьЩЯПЮЪБЃЌЭѕРЯЪІдкЭъШЋВЛжЊЕРФФИіПЊЙиЖдгІПижЦФФХХШеЙтЕЦЕФЧщПіЯТЯШКѓЫцЛњАДЯТСНИіПЊЙиЃЎ
ЃЈ1ЃЉЧѓЭѕРЯЪІАДЯТЕквЛИіПЊЙиЧЁКУФмДђПЊЕквЛХХШеЙтЕЦЕФИХТЪЃЛ
ЃЈ2ЃЉЭѕРЯЪІАДЯТСНИіПЊЙиЧЁКУФмДђПЊЕквЛХХгыЕкШ§ХХШеЙтЕЦЕФИХТЪЪЧЖрЩйЃПЧыСаБэИёЛђЛЪїзДЭММгвдЗжЮіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЃЈвЛЃЉШчЙћСНИіКЏЪ§y1ЃЌy2ЃЌДцдкxШЁЭЌвЛИіжЕЃЌЪЙЕУy1ЃНy2ЃЌФЧУДГЦy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌГЦЖдгІxЕФжЕЮЊy1ЃЌy2ЕФЁАКЯзїЕуЁБЃЛЃЈЖўЃЉШчЙћСНИіКЏЪ§ЮЊy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌФЧУДy1+y2ЕФзюДѓжЕГЦЮЊy1ЃЌy2ЕФЁАЙВгЎжЕЁБЃЎ
ЃЈ1ЃЉХаЖЯКЏЪ§yЃН2x+4mгыyЃН![]() ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉХаЖЯКЏЪ§yЃН2x+4mгыyЃНxЉ1ЃЈ|x|Ём2ЃЉЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉвбжЊКЏЪ§yЃНx+2mгыyЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЈ0ЁмxЁм5ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЌЧвгаЮЈвЛЁАКЯзїЕуЁБЃЎ
ЂйЧѓГіmЕФШЁжЕЗЖЮЇЃЛ
ЂкШєЫќУЧЕФЁАЙВгЎжЕЁБЮЊ24ЃЌЪдЧѓГіmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com