
°æƒø°ø∂®“£∫£®“ª£©»Áπ˚¡Ω∏ˆ∫Ø ˝y1£¨y2£¨¥Ê‘⁄x»°Õ¨“ª∏ˆ÷µ£¨ πµ√y1£Ωy2£¨ƒ«√¥≥∆y1£¨y2Œ™°∞∫œ◊˜∫Ø ˝°±£¨≥∆∂‘”¶xµƒ÷µŒ™y1£¨y2µƒ°∞∫œ◊˜µ„°±£ª£®∂˛£©»Áπ˚¡Ω∏ˆ∫Ø ˝Œ™y1£¨y2Œ™°∞∫œ◊˜∫Ø ˝°±£¨ƒ«√¥y1+y2µƒ◊Ó¥Û÷µ≥∆Œ™y1£¨y2µƒ°∞π≤”Æ÷µ°±£Æ
£®1£©≈–∂œ∫Ø ˝y£Ω2x+4m”Îy£Ω![]() «∑ÒŒ™°∞∫œ◊˜∫Ø ˝°±£¨»Áπ˚ «£¨«Î«Û≥ˆm£Ω1 ±À¸√«µƒ°∞∫œ◊˜µ„°±£ª»Áπ˚≤ª «£¨«ÎÀµ√˜¿Ì”…£ª
«∑ÒŒ™°∞∫œ◊˜∫Ø ˝°±£¨»Áπ˚ «£¨«Î«Û≥ˆm£Ω1 ±À¸√«µƒ°∞∫œ◊˜µ„°±£ª»Áπ˚≤ª «£¨«ÎÀµ√˜¿Ì”…£ª
£®2£©≈–∂œ∫Ø ˝y£Ω2x+4m”Îy£Ωx©Å1£®|x|°Ð2£© «∑ÒŒ™°∞∫œ◊˜∫Ø ˝°±£¨»Áπ˚ «£¨«Î«Û≥ˆ°∞∫œ◊˜µ„°±£ª»Áπ˚≤ª «£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©“—÷™∫Ø ˝y£Ωx+2m”Îy£Ωx2©Å£®2m+1£©x+£®m2+4m©Å3£©£®0°Ðx°Ð5£© «°∞∫œ◊˜∫Ø ˝°±£¨«“”–Œ®“ª°∞∫œ◊˜µ„°±£Æ
¢Ÿ«Û≥ˆmµƒ»°÷µ∑∂Œß£ª
¢⁄»ÙÀ¸√«µƒ°∞π≤”Æ÷µ°±Œ™24£¨ ‘«Û≥ˆmµƒ÷µ£Æ
°æ¥∞∏°ø£®1£© «£¨x£Ω©Å3ªÚx£Ω1£ª£®2£©≤ª «£¨º˚Ω‚Œˆ£ª£®3£©¢Ÿ©Å3°Ðm£º1ªÚ2£ºm°Ð6£ª¢⁄m£Ω2©Å![]() ªÚm£Ω3£Æ
ªÚm£Ω3£Æ
°æΩ‚Œˆ°ø
£®1£©”…”⁄![]() ”Î
”Î![]() ∂ºæ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞ£¨À˘“‘¡Ω∏ˆ∫Ø ˝”–π´π≤µ„£¨ø…“‘≈–∂œ¡Ω∏ˆ∫Ø ˝ «°∞∫œ◊˜∫Ø ˝°±£¨‘Ÿ¡™¡¢
∂ºæ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞ£¨À˘“‘¡Ω∏ˆ∫Ø ˝”–π´π≤µ„£¨ø…“‘≈–∂œ¡Ω∏ˆ∫Ø ˝ «°∞∫œ◊˜∫Ø ˝°±£¨‘Ÿ¡™¡¢![]() £¨Ω‚µ√
£¨Ω‚µ√![]() ªÚ
ªÚ![]() £¨º¥ø…«Û°∞∫œ◊˜µ„°±£ª
£¨º¥ø…«Û°∞∫œ◊˜µ„°±£ª
£®2£©ºŸ…Ë «°∞∫œ◊˜∫Ø ˝°±£¨ø…«Û°∞∫œ◊˜µ„°±Œ™![]() £¨‘Ÿ”…
£¨‘Ÿ”…![]() £¨ø…µ√µ±
£¨ø…µ√µ±![]() ±£¨ «°∞∫œ◊˜∫Ø ˝°±£ªµ±
±£¨ «°∞∫œ◊˜∫Ø ˝°±£ªµ±![]() ªÚ
ªÚ![]() ±£¨≤ª «°∞∫œ◊˜∫Ø ˝°±£ª
±£¨≤ª «°∞∫œ◊˜∫Ø ˝°±£ª
£®3£©¢Ÿ”…“—÷™ø…µ√£∫![]() £¨Ω‚µ√
£¨Ω‚µ√![]() ªÚ
ªÚ![]() £¨‘Ÿ”…“—÷™ø…µ√µ±
£¨‘Ÿ”…“—÷™ø…µ√µ±![]() ±£¨
±£¨![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() £¨“ÚŒ™÷ª”–“ª∏ˆ°∞∫œ◊˜µ„°±‘Ú
£¨“ÚŒ™÷ª”–“ª∏ˆ°∞∫œ◊˜µ„°±‘Ú![]() ªÚ
ªÚ![]() £ª¢⁄
£ª¢⁄![]() £¨”…¢Ÿø…∑÷¡Ω÷÷«Èøˆ«Û
£¨”…¢Ÿø…∑÷¡Ω÷÷«Èøˆ«Û![]() µƒ÷µ£∫µ±
µƒ÷µ£∫µ±![]() ±£¨
±£¨![]() ±£¨
±£¨![]() ‘⁄
‘⁄![]() µƒ”–◊Ó¥Û÷µŒ™
µƒ”–◊Ó¥Û÷µŒ™![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() ±£¨
±£¨![]() ‘⁄
‘⁄![]() µƒ”–◊Ó¥Û÷µŒ™
µƒ”–◊Ó¥Û÷µŒ™![]() £¨∑÷±«Û≥ˆ∑˚∫œÃıº˛µƒ
£¨∑÷±«Û≥ˆ∑˚∫œÃıº˛µƒ![]() ÷µº¥ø…£Æ
÷µº¥ø…£Æ
Ω‚£∫£®1£©![]() «æ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞµƒ÷±œþ£¨
«æ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞµƒ÷±œþ£¨![]() «æ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞµƒÀ´«˙œþ£¨
«æ≠π˝µ⁄“ª°¢µ⁄»˝œÛœÞµƒÀ´«˙œþ£¨
![]() ¡Ω∫Ø ˝”–π´π≤µ„£¨
¡Ω∫Ø ˝”–π´π≤µ„£¨
![]() ¥Ê‘⁄
¥Ê‘⁄![]() »°Õ¨“ª∏ˆ÷µ£¨ πµ√
»°Õ¨“ª∏ˆ÷µ£¨ πµ√![]() £¨
£¨
![]() ∫Ø ˝
∫Ø ˝![]() ”Î
”Î![]() «°∞∫œ◊˜∫Ø ˝°±£ª
«°∞∫œ◊˜∫Ø ˝°±£ª
µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() £¨Ω‚µ√
£¨Ω‚µ√![]() ªÚ
ªÚ![]() £¨
£¨
![]() °∞∫œ◊˜µ„°±Œ™
°∞∫œ◊˜µ„°±Œ™![]() ªÚ
ªÚ![]() £ª
£ª
£®2£©ºŸ…Ë∫Ø ˝![]() ”Î
”Î![]() «°∞∫œ◊˜∫Ø ˝°±£¨
«°∞∫œ◊˜∫Ø ˝°±£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
![]() µ±
µ±![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() ”Î
”Î![]() «°∞∫œ◊˜∫Ø ˝°±£ªµ±
«°∞∫œ◊˜∫Ø ˝°±£ªµ±![]() ªÚ
ªÚ![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() ”Î
”Î![]() ≤ª «°∞∫œ◊˜∫Ø ˝°±£ª
≤ª «°∞∫œ◊˜∫Ø ˝°±£ª
£®3£©¢Ÿ![]() ∫Ø ˝
∫Ø ˝![]() ”Î
”Î![]() «°∞∫œ◊˜∫Ø ˝°±£¨
«°∞∫œ◊˜∫Ø ˝°±£¨
![]() £¨
£¨
![]() £¨
£¨
![]() ªÚ
ªÚ![]() £¨
£¨
![]() ±”–Œ®“ª∫œ◊˜µ„£¨
±”–Œ®“ª∫œ◊˜µ„£¨
µ±![]() ±£¨
±£¨![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() ªÚ
ªÚ![]() ±£¨¬˙◊„“‚£ª
±£¨¬˙◊„“‚£ª
¢⁄![]() £¨
£¨
![]() ∂‘≥∆÷·Œ™
∂‘≥∆÷·Œ™![]() £¨
£¨
![]() ªÚ
ªÚ![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() ±£¨
±£¨![]() ‘⁄
‘⁄![]() µƒ”–◊Ó¥Û÷µŒ™
µƒ”–◊Ó¥Û÷µŒ™![]() £¨
£¨
![]() £¨
£¨
![]() ªÚ
ªÚ![]() £¨
£¨
![]() £ª
£ª
µ±![]() ±£¨
±£¨![]() ±£¨
±£¨![]() ‘⁄
‘⁄![]() µƒ”–◊Ó¥Û÷µŒ™
µƒ”–◊Ó¥Û÷µŒ™![]() £¨
£¨
![]() £¨
£¨
![]() ªÚ
ªÚ![]() £¨
£¨
![]() £ª
£ª
◊€…œÀ˘ ˆ£∫![]() ªÚ
ªÚ![]() £Æ
£Æ


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄≥ı÷–Ω◊∂Œµƒ∫Ø ˝—ßœ∞÷–£¨Œ“√«æ≠¿˙¡À¡–±Ì°¢√˵„°¢¡¨œþª≠∫Ø ˝ÕºœÛ£¨≤¢Ω·∫œÕºœÛ—–æø∫Ø ˝–‘÷ µƒπ˝≥ãƓ‘œ¬ «Œ“√«—–æø∫Ø ˝![]() –‘÷ º∞∆‰”¶”√µƒ≤ø∑÷π˝≥㨫Î∞¥“™«ÛÕÍ≥…œ¬¡–∏˜–°Ã‚£Æ
–‘÷ º∞∆‰”¶”√µƒ≤ø∑÷π˝≥㨫Î∞¥“™«ÛÕÍ≥…œ¬¡–∏˜–°Ã‚£Æ
£®1£©«Î∞—œ¬±Ì≤π≥‰ÕÍ’˚£¨≤¢‘⁄Õº÷–≤π»´∏√∫Ø ˝ÕºœÛ£ª
| °≠ | £≠5 | £≠4 | £≠3 | £≠2 | £≠1 | 0 | 1 | 2 | 3 | 4 | 5 | °≠ |
| °≠ |
|
|
| £≠3 | 0 | 3 |
|
|
| °≠ |
£®2£©∏˘æð∫Ø ˝ÕºœÛ£¨≈–∂œœ¬¡–πÿ”⁄∏√∫Ø ˝–‘÷ µƒÀµ∑® «∑Ò’˝»∑£¨’˝»∑µƒ‘⁄œý”¶µƒ¿®∫≈ƒ⁄¥Ú°∞°Ã°±£¨¥ÌŒÛµƒ‘⁄œý”¶µƒ¿®∫≈ƒ⁄¥Ú°∞°¡°±£ª
¢Ÿ∏√∫Ø ˝ÕºœÛ «÷·∂‘≥∆Õº–Œ£¨À¸µƒ∂‘≥∆÷·Œ™y÷·£ª( )
¢⁄∏√∫Ø ˝‘⁄◊‘±‰¡øµƒ»°÷µ∑∂Œßƒ⁄£¨”–◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£¨µ±![]() ±£¨∫Ø ˝»°µ√◊Ó¥Û÷µ3£ªµ±
±£¨∫Ø ˝»°µ√◊Ó¥Û÷µ3£ªµ±![]() ±£¨∫Ø ˝»°µ√◊Ó–°÷µ£≠3£ª( )
±£¨∫Ø ˝»°µ√◊Ó–°÷µ£≠3£ª( )
¢€µ±![]() ªÚ
ªÚ![]() ±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ªµ±
±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ªµ±![]() ±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª( )
±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª( )
£®3£©“—÷™∫Ø ˝![]() µƒÕºœÛ»ÁÕºÀ˘ æ£¨Ω·∫œƒ„À˘ª≠µƒ∫Ø ˝ÕºœÛ£¨÷±Ω”–¥≥ˆ≤ªµ» Ω
µƒÕºœÛ»ÁÕºÀ˘ æ£¨Ω·∫œƒ„À˘ª≠µƒ∫Ø ˝ÕºœÛ£¨÷±Ω”–¥≥ˆ≤ªµ» Ω![]() µƒΩ‚ºØ£®±£¡Ù1Œª–° ˝£¨ŒÛ≤Ó≤ª≥¨π˝0.2£©£Æ
µƒΩ‚ºØ£®±£¡Ù1Œª–° ˝£¨ŒÛ≤Ó≤ª≥¨π˝0.2£©£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ª¥Œ∫Ø ˝y£Ωk1x+bµƒÕºœÛ”Îx÷·°¢y÷·∑÷±Ωª”⁄A£¨B¡Ωµ„£¨”Î∑¥±»¿˝∫Ø ˝y£Ω![]() µƒÕºœÛ∑÷±Ωª”⁄C£¨D¡Ωµ„£¨µ„C£®2£¨4£©£¨µ„B «œþ∂ŒACµƒ÷–µ„£Æ
µƒÕºœÛ∑÷±Ωª”⁄C£¨D¡Ωµ„£¨µ„C£®2£¨4£©£¨µ„B «œþ∂ŒACµƒ÷–µ„£Æ
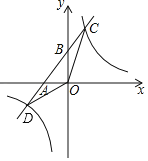
£®1£©«Û“ª¥Œ∫Ø ˝y£Ωk1x+b”Î∑¥±»¿˝∫Ø ˝y£Ω![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©«Û°˜CODµƒ√ʪ˝£ª
£®3£©÷±Ω”–¥≥ˆµ±x»° ≤√¥÷µ ±£¨k1x+b£º![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£◊È÷Ø»´–£—ß…˙Ω¯––¡À“ª¥Œ°∞…Áª·÷˜“Â∫À–ƒº€÷µπ€°±÷™ ∂æ∫»¸£¨»¸∫ÛÀʪ˙≥È»°¡À∏˜ƒÍº∂≤ø∑÷—ß…˙≥…º®Ω¯––Õ≥º∆£¨÷∆◊˜»Áœ¬∆µ ˝∑÷≤º±Ì∫Õ∆µ ˝∑÷≤º÷±∑ΩÕº£Æ«Î∏˘æðÕº±Ì÷–Ã·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
∑÷ ˝∂Œ£® | ∆µ ˝ | ∆µ¬ |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
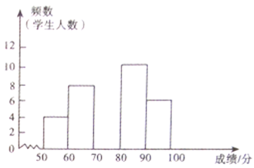
£®1£©«Î«Û≥ˆ∏√–£Àʪ˙≥È»°¡À____—ß…˙≥…º®Ω¯––Õ≥º∆£ª
£®2£©±Ì÷–![]() ____£¨
____£¨![]() ____£¨≤¢≤π»´÷±∑ΩÕº£ª
____£¨≤¢≤π»´÷±∑ΩÕº£ª
£®3£©»Ù”√…»–ŒÕ≥º∆Õº√Ë ˆ¥À≥…º®Õ≥º∆∑÷≤º«Èøˆ£¨‘Ú∑÷ ˝∂Œ![]() ∂‘”¶…»–Œµƒ‘≤–ƒΩ«∂» ˝ «___
∂‘”¶…»–Œµƒ‘≤–ƒΩ«∂» ˝ «___![]() £ª
£ª
£®4£©»Ù∏√–£π≤”–—ß…˙8000»À£¨«Îπ¿º∆∏√–£∑÷ ˝‘⁄![]() µƒ—ß…˙”–∂ý…Ÿ»À£ø
µƒ—ß…˙”–∂ý…Ÿ»À£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„MŒ™À´«˙œþy£Ω![]() …œ“ªµ„£¨π˝µ„M◊˜x÷·°¢y÷·µƒ¥πœþ£¨∑÷±Ωª÷±œþy£Ω©Åx+2m”⁄D°¢C¡Ωµ„£¨»Ù÷±œþy£Ω©Åx+2mΩªy÷·”⁄A£¨Ωªx÷·”⁄B£¨‘ÚADBCµƒ÷µŒ™_____£Æ
…œ“ªµ„£¨π˝µ„M◊˜x÷·°¢y÷·µƒ¥πœþ£¨∑÷±Ωª÷±œþy£Ω©Åx+2m”⁄D°¢C¡Ωµ„£¨»Ù÷±œþy£Ω©Åx+2mΩªy÷·”⁄A£¨Ωªx÷·”⁄B£¨‘ÚADBCµƒ÷µŒ™_____£Æ
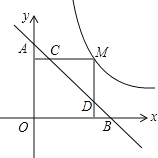
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°œA=°œB£¨AE=BE£¨µ„D‘⁄AC±þ…œ£¨°œ1=°œ2£¨AE∫ÕBDœýΩª”⁄µ„O£Æ

£®1£©«Û÷§£∫°˜AEC°’°˜BED£ª
£®2£©»Ù°œ1=42°„£¨«Û°œBDEµƒ∂» ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ùπÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ãx2+£®2k©Å1£©x+k2=0µƒ¡Ω∏˘a°¢b¬˙◊„a2©Åb2=0£¨À´«˙œþ![]() £®x£æ0£©æ≠π˝Rt°˜OAB–±±þOBµƒ÷–µ„D£¨”Î÷±Ω«±þABΩª”⁄C£®»ÁÕº£©£¨‘ÚS°˜OBCŒ™£®°°°°£©
£®x£æ0£©æ≠π˝Rt°˜OAB–±±þOBµƒ÷–µ„D£¨”Î÷±Ω«±þABΩª”⁄C£®»ÁÕº£©£¨‘ÚS°˜OBCŒ™£®°°°°£©
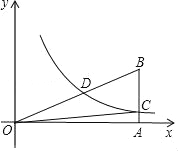
A. 3 B. ![]() C. 6 D. 3ªÚ
C. 6 D. 3ªÚ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù![]() ∫Õ
∫Õ![]() æ˘Œ™µ»—¸»˝Ω«–Œ£¨«“
æ˘Œ™µ»—¸»˝Ω«–Œ£¨«“![]() £Æ
£Æ
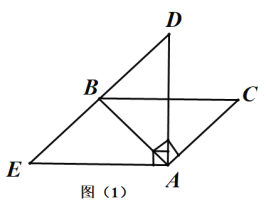
£®1£©»ÁÕº£®1£©£¨µ„B «![]() µƒ÷–µ„£¨≈–∂®Àƒ±þ–Œ
µƒ÷–µ„£¨≈–∂®Àƒ±þ–Œ![]() µƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
µƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
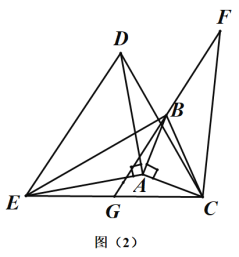
£®2£©»ÁÕº£®2£©£¨»Ùµ„G «![]() µƒ÷–µ„£¨¡¨Ω”
µƒ÷–µ„£¨¡¨Ω”![]() ≤¢—”≥§÷¡µ„F£¨ π
≤¢—”≥§÷¡µ„F£¨ π![]() £Æ«Û÷§£∫¢Ÿ
£Æ«Û÷§£∫¢Ÿ![]() £¨¢⁄
£¨¢⁄![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
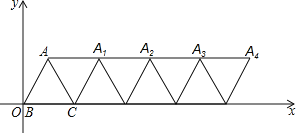
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµƒ⁄£¨±þ≥§Œ™4µƒµ»±þ![]() µƒ∂•µ„
µƒ∂•µ„![]() ”Α≠µ„÷ÿ∫œ£¨Ω´
”Α≠µ„÷ÿ∫œ£¨Ω´![]() »∆∂•µ„
»∆∂•µ„![]() À≥ ±’Ζ˝◊™
À≥ ±’Ζ˝◊™![]() µƒ
µƒ![]() Ω´Àƒ±þ–Œ
Ω´Àƒ±þ–Œ![]() ø¥◊˜“ª∏ˆª˘±æÕº–Œ£¨Ω´¥Àª˘±æÕº–Œ≤ª∂œ∏¥÷∆≤¢∆Ω“∆£¨‘Ú
ø¥◊˜“ª∏ˆª˘±æÕº–Œ£¨Ω´¥Àª˘±æÕº–Œ≤ª∂œ∏¥÷∆≤¢∆Ω“∆£¨‘Ú![]() µƒ◊¯±ÍŒ™__________£Æ
µƒ◊¯±ÍŒ™__________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com