
【题目】一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同.
(1)搅匀后,从中任意摸出一个球,恰好是红球的概率是 ;
(2)搅匀后,从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球.
①求两次都摸到红球的概率;
②经过了n次“摸球﹣记录﹣放回”的过程,全部摸到红球的概率是 .
【答案】(1)![]() ;(2)①P(B)=
;(2)①P(B)=![]() ;②(
;②( ![]() )n.
)n.
【解析】试题分析:
(1)由题意易可知,共有3种等可能结果,其中是红球的占了2种,由此可得所求概率为![]() ;
;
(2)①画树状图分析出所有的等可能结果,看其中两次都是红球的有多少种,即可得到所求概率;②由题意可知,摸一次有3种等可能结果,放回摸第2次后共有9种等可能结果,……,摸n次后共有![]() 个等可能结果,其中全是红球的有
个等可能结果,其中全是红球的有![]() 种,由此即可得到所求概率.
种,由此即可得到所求概率.
试题解析:
(1)∵一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,
∴搅匀后,从中任意摸出一个球,恰好是红球的概率是: ![]() ;
;
故答案为: ![]() .
.
(2)①画树状图得:
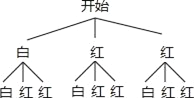
∵共有9种,它们出现的可能性相同.所有的结果中,满足“两次都是红球”(记为事件B)的结果只有4种,
P(B)=![]() ;
;
②∵经过了n次“摸球﹣记录﹣放回”的过程,共有3n种等可能的结果,全部摸到红球的有2n种情况,
∴全部摸到红球的概率是:(![]() )n.
)n.
故答案为:(![]() )n.
)n.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
A. y1>y2>y3B. y2>y1>y3C. y3>y1>y2D. y3>y2>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学复习课上,张老师出示了下框中的问题:
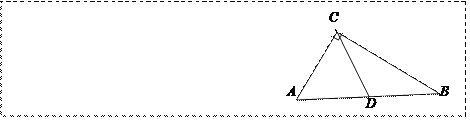
已知:在Rt△ACB中,∠C=90°,点D是斜边AB上的中点,连接CD.
求证:CD=![]() AB.
AB.
问题思考
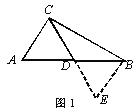
(1)经过独立思考,同学们想出了多种正确的证明思想,其中有位同学的思路如下:如图1,过点B作BE∥AC交CD的延长线于点E。请你根据这位同学的思路提示证明上述框中的问题.
方法迁移
(2)如图2,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC上一动点,连接DE,线段DF始终与DE垂直且交BC于点F。试猜想线段AE,EF,BF之间的数量关系,并加以证明.
拓展延伸
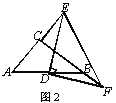
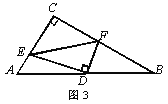
(3)如图3,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC延长线上一动点,连接DE,线段DF始终与DE垂直且交CB延长线于点F。试问第(2)小题中线段AE,EF,BF之间的数量关系会发生改变吗?若会,请写出关系式;若不会,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.
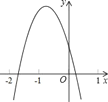
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出直线![]() 的图象,并解答下列问题:
的图象,并解答下列问题:
(1)设它的图象与y轴、x轴分别交于点A、B,求AB的长;
(2)求![]() 的周长(O为坐标原点);
的周长(O为坐标原点);
(3)求点O到直线AB的距离;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列资料,解决问题:
定义:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:![]() ,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:![]() 这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:![]() .
.
(1)分式![]() 是 (填“真分式”或“假分式”);
是 (填“真分式”或“假分式”);
(2)将假分式![]() 分别化为带分式;
分别化为带分式;
(3)如果分式![]() 的值为整数,求所有符合条件的整数x的值.
的值为整数,求所有符合条件的整数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com